#Desafio 12: Solução
Um quadrado foi dividido em 7 quadradinhos congruentes e 2 triângulos congruentes. Se a área do quadradinho sombreado é de 4 cm², qual a área do triângulo sombreado?

O desafio de hoje se apresenta de maneira muito simples quanto a suas formas de resolução. Espero de verdade que você tenha tentado resolvê-lo e sem mais delongas, VAMOS LÁ!
Método 01: Determine os comprimentos de alguns segmentos.
Sabendo que o quadradinho laranja possui área de 4 cm², podemos concluir que a medida de seus lados seja de 2 cm.
Por isso, fica fácil perceber que o quadrado maior tem lado três vezes maior do que o lado de um quadradinho, logo possui lado de medida 6 cm.
Como o triângulo ciano ocupa metade da área do quadrado, podemos calcular a área dele da seguinte forma:
Método 02: Comparando áreas entre diferentes quadrados.
Se utilizarmos o quadradinho laranja destacado, o qual nós já conhecemos a área, como nosso padrão de medida, nossa unidade de medida, poderemos sobrepor o quadrado utilizando algumas cópias desta figura.
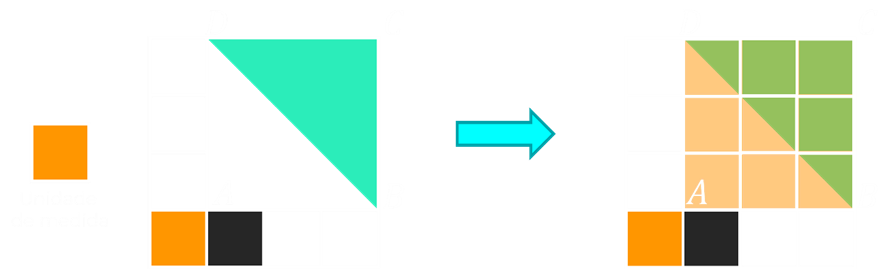
Dessa forma, podemos ver que serão necessários nove quadradinhos. Como a área de cada quadradinho é igual a 4 cm², fica fácil perceber que a área do quadrado {ABCD} é de:
E como o segmento {\overline{AC}} divide o quadrado {ABCD} em dois triângulos de áreas iguais, logo o triângulo sombreado {BCD} tem área igual a 18 cm².
E você, tinha conseguido resolver este desafio? Como você fez? Espero que tenham gostado das soluções propostas.
Até a próxima.



