As abelhas e os favos hexagonais

Na sexta – feira, dia 03 de setembro de 2021, algumas abelhas resolveram fazer uma paradinha aqui em casa. Elas decidiram ocupar toda a lavanderia o armário da lavanderia até sábado de manhã, quando decidiram seguir viagem. Foi algo bem inesperado por todo mundo! Ainda bem que ninguém se machucou. Mas existe algo que me fez retomar uma dúvida a respeito das abelhas que há tempos, já havia me ocorrido: Por que os favos construídos pelas abelhas têm formatos hexagonais?

Pois então eu convido você a refletir comigo sobre esse interessante fato, e para isso precisaremos de um pouco de geometria.

Para a construção dos alvéolos, que são aquelas estruturas que conhecemos com formato hexagonal e que compõem o favo, as abelhas usam um tipo de cera, que é uma substância de cor branca, secretada por glândulas cerígenas de abelhas operárias jovens e são moldadas na forma de pequenas placas.

Para a modelagem da cera, as abelhas utilizam o calor do próprio corpo e constroem uma estrutura cilíndrica, onde serão armazenados mel ou células de cria. Vale lembrar que cada espaço possuí certa profundidade, mas por enquanto estamos interessados somente no formato das bases. Quando a cera esfria a estrutura se contrai e os círculos, “acidentalmente”, adquirem formatos hexagonais.

Mas por que tinham que ser um hexágono? Não poderia ser um octógono? heptágono? Quem sabe até um dodecágono?!

Pois bem, acontece que existem polígonos regulares que podem formar padrões que recobrem uma região plana e polígonos que não. Esses padrões são chamados de mosaicos do plano. Para que essa análise seja feita vamos impor algumas condições para que todo mosaico seja construído seguindo o mesmo padrão:

I. Dois polígonos regulares devem possuir um lado ou um vértice em comum;
II. A alocação dos polígonos regulares em torno de cada vértice deve ser sempre a mesma;

Essas condições servirão para que, em cada tentativa de recobrimento com qualquer que seja o polígono, nós tenhamos uma regra a seguir. Em um mosaico, a soma das medidas dos ângulos internos que se unem em um ponto (através do vértice desse polígono regular) tem que resultar em 360° para que não haja lacunas nem sobreposições entre as figuras.

Com isso, sabemos que a medida do ângulo interno do polígono regular precisa ser um divisor de 360°.

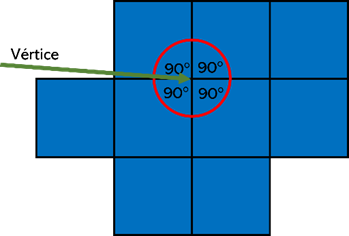
Para descobrirmos a medida de um ângulo interno de qualquer polígono regular podemos recorrer a um transferidor ou à uma fórmula. Vale lembrar que neste artigo só faremos uso da fórmula e não iremos demonstrá-la.

Onde {n} representa o número de lados do polígono.

Utilizando a fórmula acima podemos tabelar algumas informações a respeito de alguns polígonos e ver quais podem recobrir um plano e quais não podem.

Mas para que nós não nos limitemos a somente seis polígonos regulares, vamos fazer uma generalização para um polígono regular de {n} lados e verificar se ele se enquadra nas características que apresentamos até aqui. A equação abaixo expressa a medida do ângulo interno de um polígono de {n} lados.

Para que o plano seja recoberto por polígonos regulares de {n} lados apenas é preciso que a medida de seu ângulo interno seja um divisor de 360°.

Onde {n} representa o número de lados do polígono e {m} representa o número de polígonos em torno de um vértice.

Trabalhando um pouco com a igualdade acima nós encontraremos a seguinte equação:

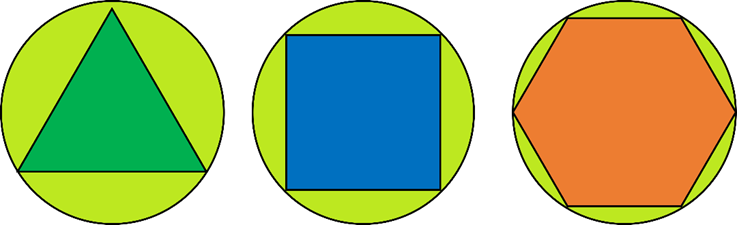
Considerando que {n\geq 3} já que o polígono com o menor número de lados é um triângulo e {m\geq 3} já que para alocar polígonos em torno de um vértice é necessário no mínimo três figuras (pensando em completar uma volta inteira, ou seja, 360°), as únicas soluções inteiras e positivas para a equação são: {n = 3} e {m = 6}; {n = 4} e {m = 4}; {n = 6} e {m = 3}.

E cada um dos pares de soluções para a equação apresentam os únicos três polígonos regulares que formam um mosaico do plano, satisfazendo as duas condições impostas inicialmente, sendo: seis triângulos equiláteros ({n = 3} e {m = 6}); quatro quadrados ({n = 4} e {m = 4}); e três hexágonos regulares ({n = 6} e {m = 3}).

Observe a representação geométrica das soluções encontradas:

Observe que na tentativa de recobrimento utilizando pentágonos regulares ficam alguns “buracos” vazios se eles se intersectarem apenas pelo lado, e ocorre sobreposição se eles se unirem por um lado e pelo vértice, mostrando que não é possível construir um mosaico utilizando esta forma geométrica.

É importante enfatizar a questão de que conseguimos utilizar mais de um tipo de polígonos (regulares ou não) em um único mosaico de maneira que não fiquem lacunas ou figuras sobrepostas. Pentágonos com lados de diferentes medidas, mas congruentes entre si são capazes de recobrir um plano, mas isso é discussão para um outro dia.

Veja a tentativa de recobrimento de outras figuras.

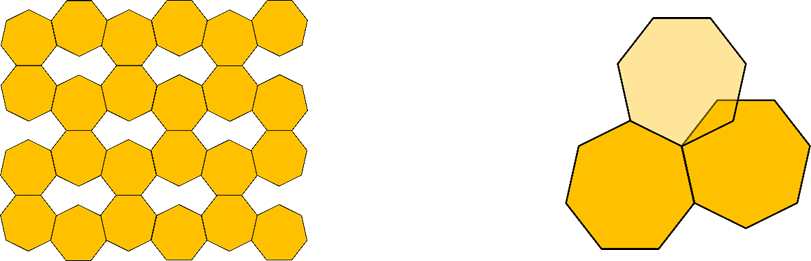
Observe que, dentre todas as tentativas de recobrimento, somente triângulos, quadrados e hexágonos conseguiram formar um mosaico sem deixar espaços vazios e sem sobrepor um ao outro. Isso deve-se a medida dos ângulos internos serem submúltiplos de 360.

Parte de nosso questionamento está respondido: os alvéolos são hexagonais, pois recobrem perfeitamente o plano (favo). Com isso nós levantamos um segundo questionamento: Por que não poderia ser um triângulo? Um quadrado?

Bem, agora iremos analisar uma segunda característica dos polígonos regulares que é a região interna delimitada pelos seus lados, em outras palavras, a área dos polígonos regulares.

Talvez você se pergunte: – “mas os favos têm profundidade. Não seria mais lógico analisar o volume?” – Bem, nós estamos nos atentando somente análise de polígonos que compõem a base desses prismas. Se levarmos em conta que o volume de um prisma é o produto da área da base pela altura, quanto mais área a base ocupar, consequentemente maior será o volume desse prisma. Por isso analisaremos a área desses três polígonos.

Inicialmente os alvéolos possuem formatos cilíndricos, ou seja, possuem um formato circular. Logo, é fácil pensar que nós só precisaremos escolher o polígono cuja área mais se aproxime da área do círculo. Se recorremos ao método da exaustão de Arquimedes para o encontro da área do círculo nós teremos a seguinte visualização:

Visualmente é fácil de verificar que os alvéolos que compõem os favos assumem o formato hexagonal pois é o único polígono regular que, pode recobrir perfeitamente um plano, e sua área é a mais próxima da de um círculo.

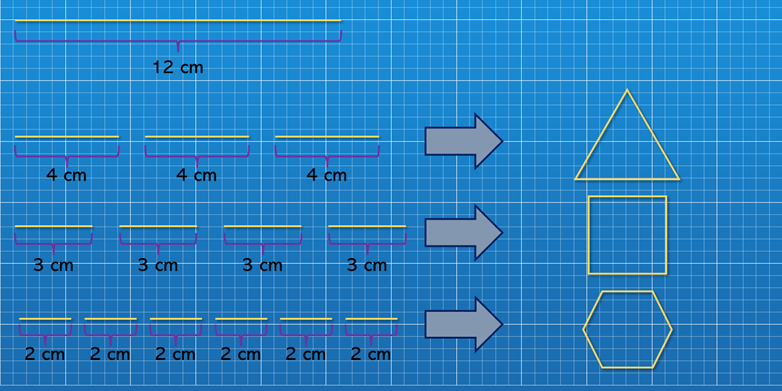
Porém irei propor uma outra reflexão para a comparação das áreas desses três polígonos sem que envolva a sobreposição de figuras. Então vamos pegar 3 varetas de bambu (ou três segmentos de reta), todos medindo 12 cm e, utilizando esse material, vamos construir os três polígonos.

Observe que a medida 12 cm foi escolhida propositalmente, pois ele é o menor múltiplo comum entre 3, 4 e 6 que são os números de lados de cada polígono. Observe que o triângulo equilátero terá lados de medida 4 cm, o quadrado terá lados de medida 3 cm e o hexágono terá medidas de 2 cm.

Fiz as marcações em palitos de churrasco com comprimento igual a 24 cm para que fosse mais fácil manuseá-los durante a montagem. A ideia se mantém.

Devido as imperfeições do material utilizado (corte, resistência, não ser totalmente retilíneo), criei uma representação digital do desenho para que melhor fosse representado a ideia com os palitos.

Agora vamos fazer uma verificação numérica a respeito das áreas dessas figuras, utilizando a fórmula para o cálculo de área de cada uma delas. Neste artigo não temos o intuito de demonstrar a fórmula de cada figura, somente de utilizá-las.

Essa tabela nos mostra que o polígono regular que abrange uma maior área utilizando o mesmo recurso para a construção de três figuras distintas, é o hexágono regular. Nós poderíamos aproximar o diâmetro do círculo inicial para 4 cm para termos uma aproximação da área original (antes da cera esfriar e contrair).

Veja que a diminuição da área de cada alvéolo é pequena e bem compreensível por conta do resfriamento de toda a estrutura do favo.

Ufa, agora deu uma sensação de trabalho cumprido. entendemos o porquê de os favos de mel possuírem uma estrutura ladrilhada de hexágono regulares, pois é a forma geométrica que otimiza a organização dos alvéolos e tira o melhor proveito no armazenamento (área), e o mais legal de pensar é que os alvéolos assumem essa forma naturalmente após o resfriamento da cera!

Bem, logo no sábado de manhã as abelhas seguiram viagem em direção a árvore da casa ao lado. Mais uma curiosidade é de que as abelhas fazem isso quando estão procurando um novo lugar para ficar, elas passam a noite em algum lugar no meio do caminho e no dia seguinte continuam sua trajetória. A melhor coisa a se fazer nesses casos é não ficar no caminho delas e esperar que saiam, caso isso não aconteça é melhor ligar para o corpo de bombeiros, ou então o armário da lavanderia da sua casa será recoberto de hexágonos regulares!

REFERÊNCIAS

Cera. Associação Brasileira de Estudos das Abelhas, 2020. Disponível em: http://abelha.org.br/cera/. Acesso em: 04 de abril de 2022

BOYD, Cindy J. et al. Geometry. McGraw-Hill Companies. 25 de março de 2003.

HELLMEISTER, Ana Catarina Pontone. Geometria em Sala de Aula. Sociedade Brasileira de Matemática. 2013.