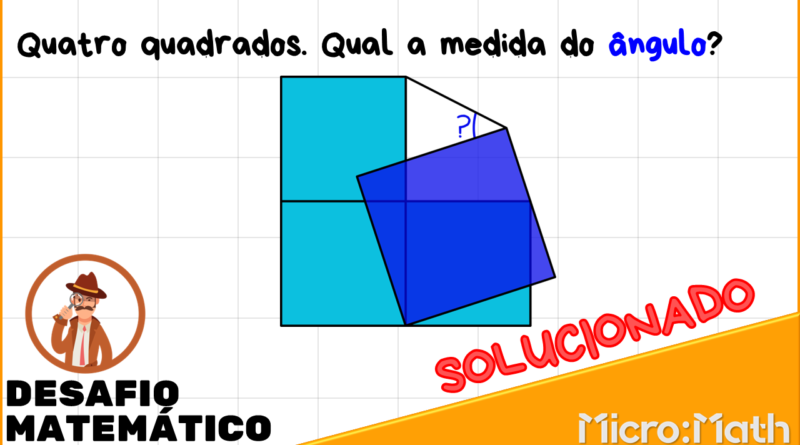
Quatro quadrados. Qual a medida do ângulo?
Este é um novo modelo de desafio matemático! Agora suas soluções serão feitas em vídeos e colocadas no meu canal do YouTube. Caso você queira ter de maneira mais visual cada uma das soluções propostas por mim, agora será possível! Este desafio foi proposto em agosto de 2020 por @cshearer41 que é uma grande professora e criadora de puzzles matemáticos!
Sem mais delongas, vamos à alguns métodos de resolução.
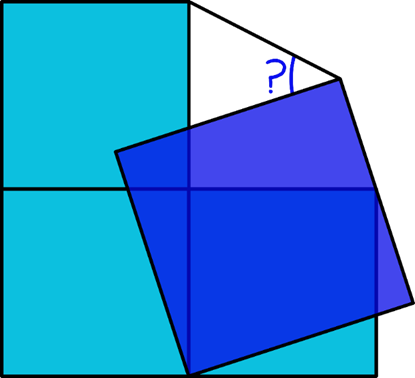
Método 01: O quinto quadrado.
Uma das primeiras soluções que encontrei para este desafio foi localizar um quinto quadrado que auxiliasse a determinação do ângulo destacado. Para isso, inicialmente, tracei as diagonais do quadrado maior. Sobre isso podemos destacar duas informações importantes.
As diagonais de um quadrado são sempre perpendiculares entre si.
As diagonais de um quadrado coincidem com as bissetrizes internas.
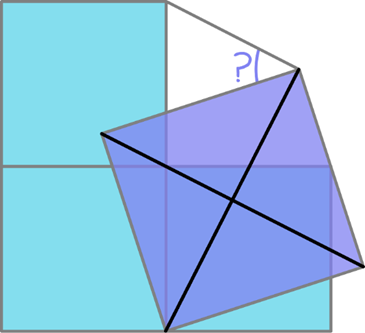
Feito isso, o quinto quadrado está quase pronto. Para finalizarmos, seria necessário traçar uma paralela a uma das diagonais do quadrado maior para fechar o quadrado.
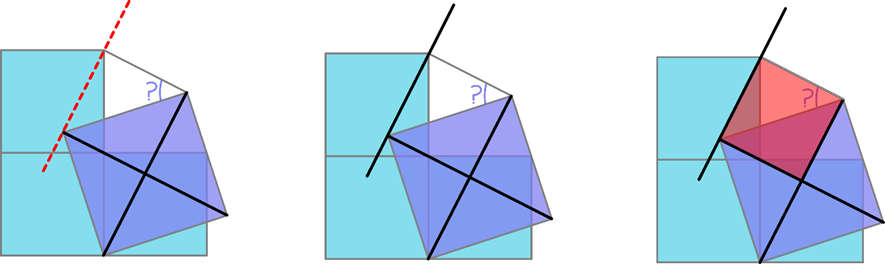
Após a construção do quinto quadrado, percebemos que um dos lados do quadrado maior faz a vez de uma das diagonais do quadrado vermelho e, como visto antes, a diagonal de um quadrado divide o ângulo interno ao meio. Se qualquer ângulo interno de um quadrado é reto, então o ângulo marcado pela interrogação mede 45°.
Método 02: Ângulos inscritos
O segundo método aparenta ser mais simples (ou pelo menos, mais direto ao ponto) do que o primeiro. Para iniciar, precisamos traçar uma circunferência centrada no vértice comum aos três quadrados menores.
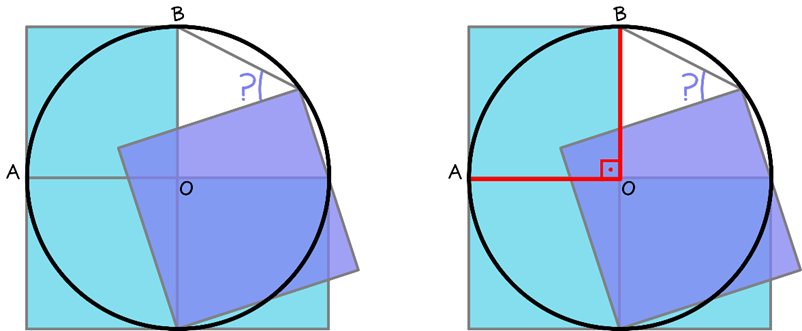
E como já adianta a figura 6, traçamos o ângulo central {\angleAOB} (coincide com um dos ângulos internos do quadrado menor superior). Poderíamos ter traçado qualquer outro ângulo interno, mas esse (necessariamente) torna os nossos próximos passos mais simples de serem concluídos, pois um dos lados do ângulo a ser determinado se
conecta com o vértice {B} do ângulo central. Dessa forma, denotarei por {C} o vértice do ângulo a ser determinado e prolongarei {\overline{AC}}. Agora o ângulo {\angle ACB} é inscrito a circunferência com relação ao ângulo central {\ angleAOB}. Como já é sabido.
Qualquer ângulo inscrito em uma circunferência tem medida igual a metade da medida do ângulo central a ele relacionado.
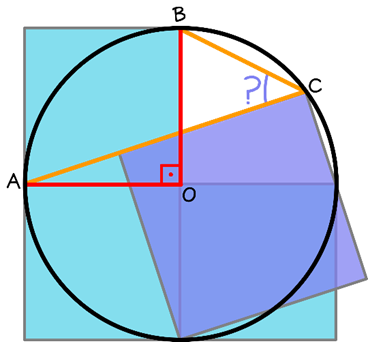
Dessa forma, é possível concluir novamente que a medida do ângulo a ser determinado é de 45°.
Obrigado a você que leu até aqui, aproveite os demais conteúdos em meu site e até semana que vem!