#Desafio 05: Solução
Os quadrados representam os algarismos 3, 4, 5 e 8 e os círculos os algarismos 1, 3, 7 e 9 em determinada ordem. Qual o número de quatro algarismos representado pelos quadrados?
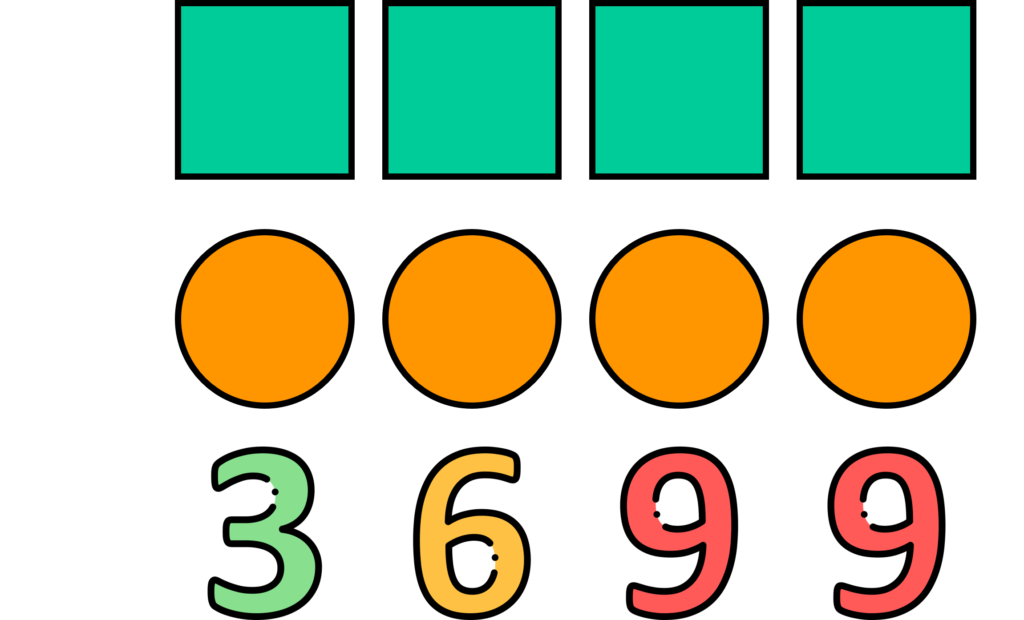
Para resolver este desafio, teremos que nos atentar muito na questão de termos números de 4 algarismos (o que por exemplo nos impediria de termos como algarismo da unidade de milhar o número 3); e no “emprestar 1”, que é desagrupar números de ordens maiores e converter para ordens menores, por isso o número {n} que estiver na ordem das dezenas terá valor {n\cdot10}; nas centenas {n\cdot100} e assim por diante.
Método 1: Pensando da direita para a esquerda.
Unidades = 8 e 9.
Dentre os números disponíveis para os quadrados e círculos, os únicos que gerariam uma diferença de 9 seriam 8 e 9. Desagrupando uma dezena do algarismo seguinte teremos:
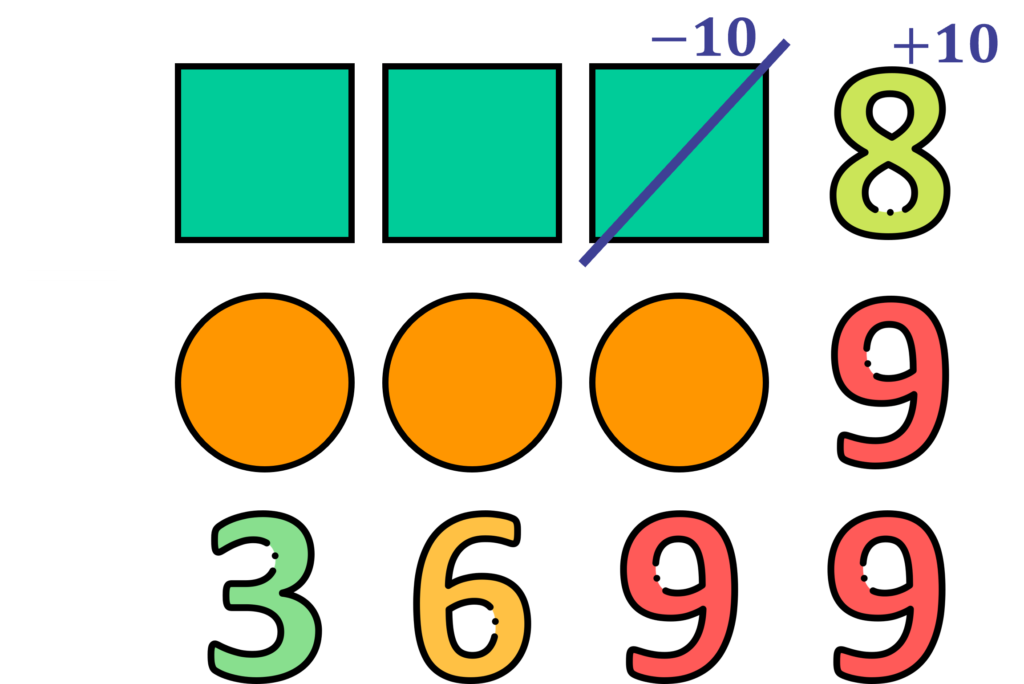
Dezenas = 3 e 3
Dentre os valores que sobraram, para obtermos novamente uma diferença igual a 9 somente se o número dos quadrados for menor do que o número dos círculos. Porém, se o círculo for 7 não encontraremos uma diferença 9, por isso precisamos que tanto o quadrado quanto o círculo das dezenas seja 3.
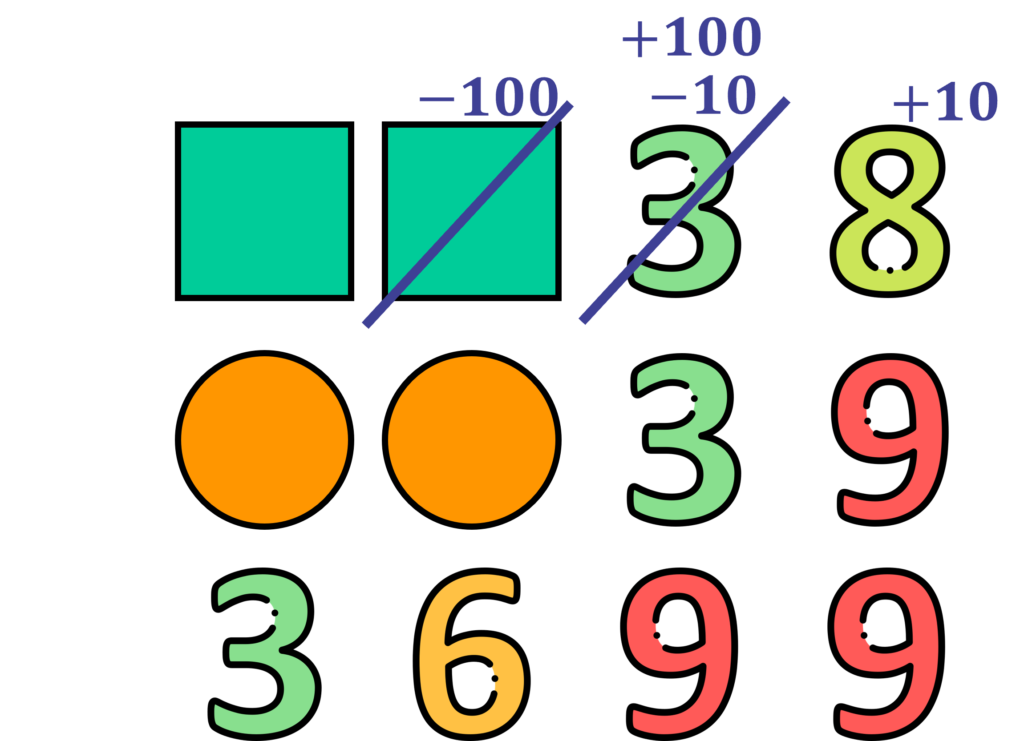
Mais uma vez relembro que estou evidenciando o real sentido do “empresta 1”, pois estou considerando os valores posicionais dos algarismos: unidades (1); dezenas (10); centenas (100); unidade de milhar (1 000).
Centenas = 4 e 7
Das opções que possuímos e da situação presente na conta, somente 4 e 7 produziriam uma diferença 6.
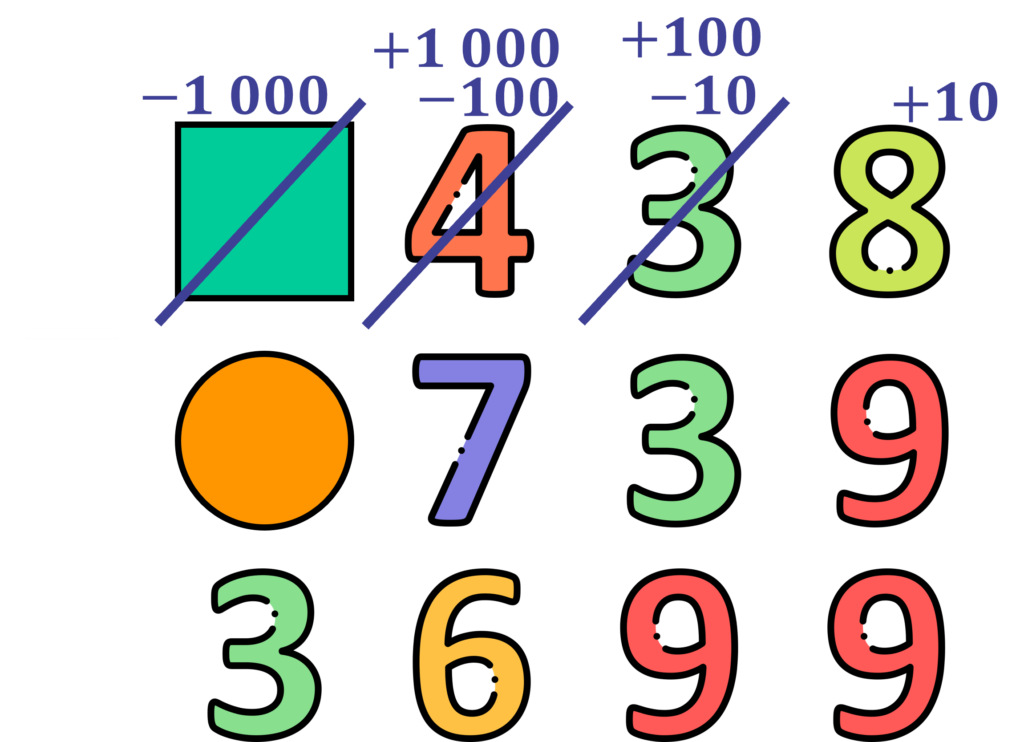
Unidades de Milhar = 5 e 1
Por eliminação, o quadrado da unidade de milhar só poderá assumir valor 5 e o círculo o valor 1.
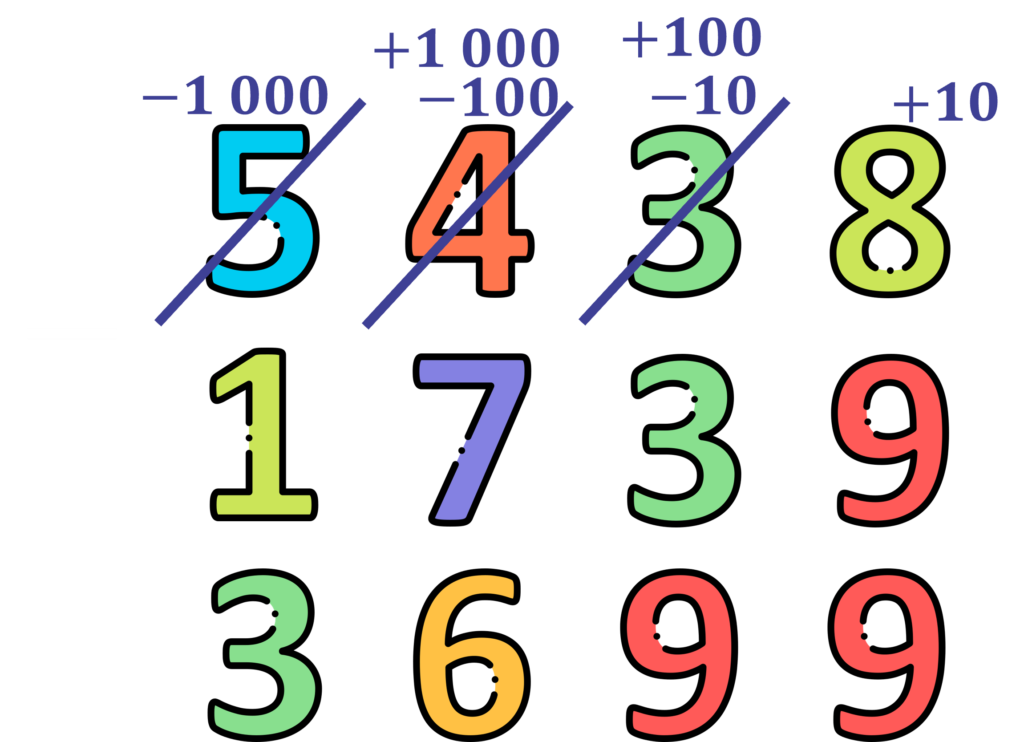
Dessa forma, os quadrados representam o número 5438.
Método 2: Transforme a subtração numa adição
Talvez seja mais fácil observar a diferença como uma adição se invertermos os papeis de alguns números.
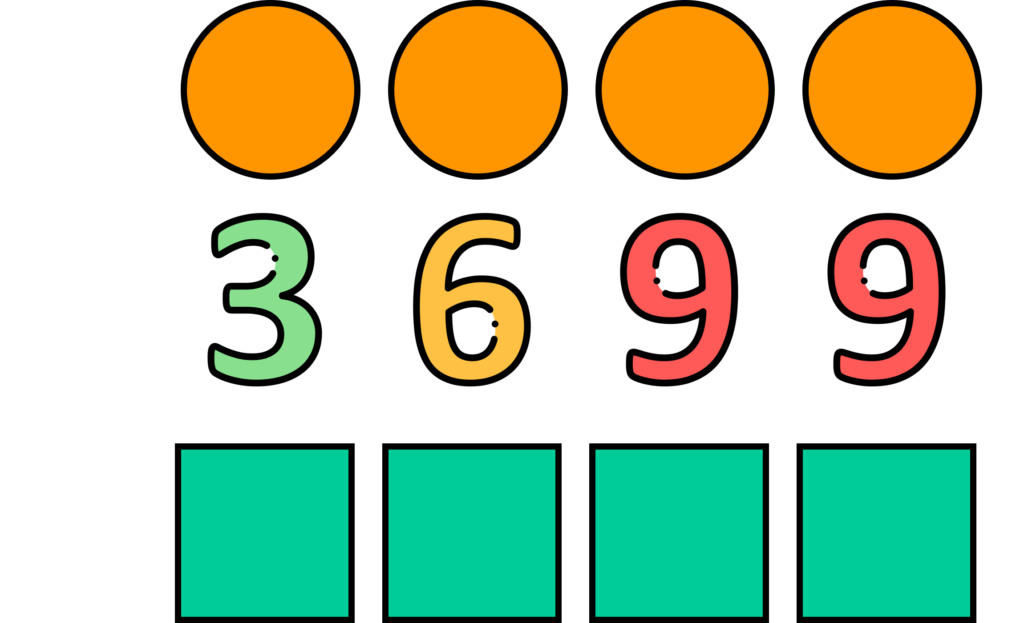
O raciocínio seria quase o mesmo, nós iríamos cair numa eliminação de possíveis somas.
Unidade:
O único número dentre os possíveis para o círculo que somado com 9 em que o algarismo das unidades fosse algum dentre os possíveis algarismos para os quadrados é o 9 que resultaria em 18.
Ficando somente o 8 para as unidades.
Dezena:
Agora nossas possibilidades precisam ser acrescidas de 1 (10, no caso da ordem das dezenas) dessa forma a possibilidade para o círculo é o 3.
Ficando somente o 30 para as dezenas.
Centena:
Da mesma forma, os algarismos serão acrescidos de 1 (100). Para o círculo teremos o 7.
Para as centenas, temos 400.
Unidade de milhar:
A única opção disponível para o círculo é o 1.
Dessa forma, o número formado pelos quadrados é:
Considerar o valor posicional dos números é sempre importante para compreendermos as operações dentro de algoritmos.
O desafio 6 já está disponível, não esqueça de dar uma conferida.