Pense em um número
Você já deve ter visto algo semelhante nas redes sociais ou algum amigo já fez esta brincadeira com você: adivinhar o número no qual você está pensando. Normalmente, alguém lhe pede para pensar em um número e depois fazer alguma coisa com ele, como somar, subtrair, multiplicar e dividir por uma série de números determinados. Então, num passe de mágica, é revelado o número obtido, embora não soubessem qual o número que você havia escolhido no começo.
Para compreender como esse truque funciona, siga as etapas a seguir:
Etapa 1: Escolha um número inteiro positivo.
Etapa 2: Adicione 3.
Etapa 3: Triplique a soma
Etapa 4: Adicione 6 ao produto
Etapa 5: Encontre a terça parte da soma.
Etapa 6: Subtraia do quociente o número escolhido no começo.
Se você fez as operações certas, sua resposta será 5.
Se acha que é mera coincidência, tente outro número. Sua resposta, após as seis etapas, sempre será 5, não importa o número escolhido.
Embora isto se assemelhe a magia, não é mágica, é matemágica!
Depois desse trocadilho sem graça, vamos tentar buscar alguma explicação. Primeiramente usarei objetos e depois uma das maiores ferramentas matemáticas que temos: a Álgebra!
Como você pode começar com qualquer número, representarei esta ideia com um saquinho de bolinhas de gude. Ninguém poderá ver o número de bolinhas contidas no saquinho.
Etapa 1: Escolha um número inteiro positivo.

Etapa 2: Adicione 3.

Etapa 3: Triplique a soma.

Etapa 4: Adicione 6 ao produto.

Etapa 5: Encontre a terça parte da soma.

Etapa 6: Subtraia do quociente o número escolhido no começo.

Utilizando os recursos visuais para passar pelas seis etapas, pudemos perceber que o número inicial escolhido pela pessoa não influi em nada no resultado. Em nenhum momento foi revelando a quantidade de bolinhas que havia dentro do saquinho.
Mas agora, no lugar desses objetos, poderemos deixar nossa representação um pouco mais sofisticada e simples. No lugar do saquinho de bolinhas de gude utilizarei a letra {n} para representar qualquer número.
Utilizar {n} como um símbolo para assegurar um lugar de um número qualquer, algumas vezes é chamado de variável. Esta é uma das ideias fundamentais de toda a álgebra.
Etapa 1: Escolha um número inteiro positivo.
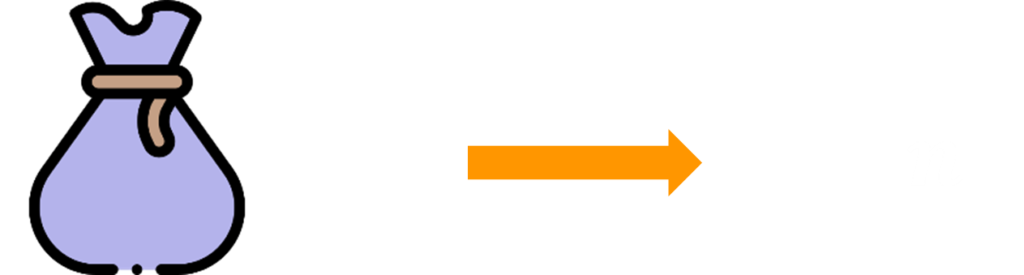
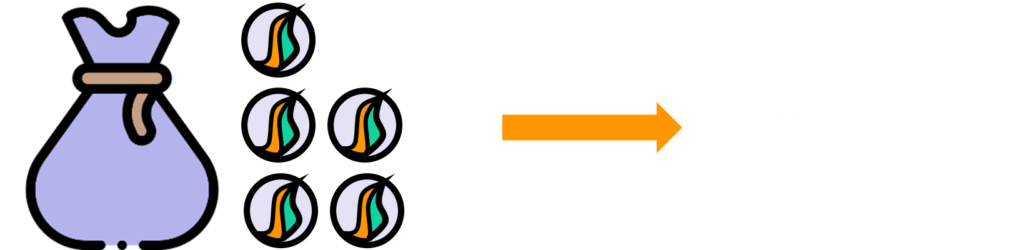
Etapa 2: Adicione 3.

Etapa 3: Triplique a soma.

Etapa 4: Adicione 6 ao produto.

Etapa 5: Encontre a terça parte da soma.
Etapa 6: Subtraia do quociente o número escolhido no começo.

Viu só? Não é tão assustador colocar letras junto de números como te contaram, não é verdade? Se consegue compreender o que ela representa e qual sua função no meio de toda a expressão fica muito simples!
Agora, podemos usar números e símbolos de operações para expressar cada etapa que ocorre neste truque.
Etapa 1: Escolha um número inteiro positivo.
Etapa 2: Adicione 3.
Etapa 3: Triplique a soma.
Etapa 4: Adicione 6 ao produto.
Etapa 5: Encontre a terça parte da soma.
Etapa 6: Subtraia do quociente o número escolhido no começo.
A expressão encontrada acima representa a combinação de todas as etapas pelas quais passamos para obter o resultado. Ela permanece igual a 5 para qualquer valor inteiro de {n}.
Vamos analisar as etapas algébricas para simplificá-la sem alterá-la. Aplicaremos primeiramente a propriedade distributiva da multiplicação com relação a adição para removermos os parênteses.
Agora podemos unir alguns termos semelhantes.
Agora poderemos efetuar a divisão de {3n+15} por 3.
Resolvendo a subtração entre os termos semelhantes, a resposta é 5.
Passo a passo, partindo de uma expressão complicada como {\frac{3(n+3)+6}{3}-n} chegamos a uma muito mais simples, 5.
A expressão do lado esquerdo é igual a expressão do lado direito para todos os valores de {n}.
Podemos ver o porquê este truque corresponde a sempre a resposta 5. Não há nenhuma adivinhação, somente princípios matemáticos.
Ao explicar esse truque, usamos uma letra, {n}, que reserva o lugar para um número qualquer. Por conta disso, este {n} é chamado de variável (pois o valor de {n} varia de pessoa para pessoa, dependendo da escolha). Aplicamos princípios básicos, como a ordem das operações e a propriedade distributiva da multiplicação com relação a adição e a subtração para realizar cálculos com expressões que continham variáveis. Esta é a Álgebra, a parte da matemática que permite generalizar raciocínios, trabalhar com ideias abstratas, resolver problemas e criar truques de adivinhação!
Espero que caso você nunca tenha ouvido falar em Álgebra, este texto possa ter mostrado que ela é muito útil e interessante para o desenvolvimento do raciocínio matemático. Caso você já tenha contato com isso, espero ter ajudado a compreender mais a funcionalidade desta parte da matemática.
Até a próxima e tudo de bom pra vocês!



