#Desafio 11: Solução

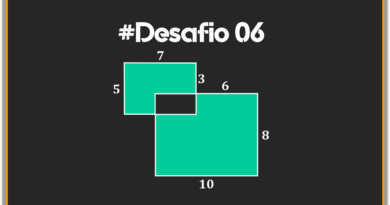
Considere as molduras hexagonais formadas por triângulos equiláteros. A 12ª moldura terá quantos triângulos equiláteros?

Hoje vamos resolver o desafio sobre as molduras hexagonais. Já disse em outros artigos do site que eu amo exercícios que apresentam sequências (no caso, recursiva), pois exercícios deste tipo nos permitem trabalhar muitos recursos matemáticos e pensar fora da caixa!

O método mais “rápido” a ser seguido seria contar de moldura em moldura para ver quantos triângulos aumentam de uma figura para outra e então descobrir quantos haveria na 12ª moldura. Mas não teria nada demais nisso, não é verdade?  Apresentarei, para este problema, três métodos de resolução! Vamos lá?

Método 01: medindo lados do hexágono.

Para uma primeira investigação, nós podemos analisar o formato hexagonal contando a quantidade de triângulos que compõe cada lado desses hexágonos.

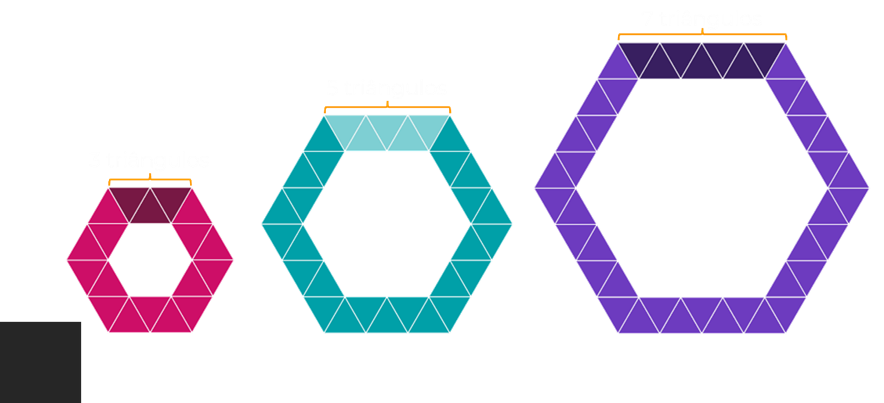
Observe que a quantidade de triângulos em cada lado é uma quantidade ímpar: 3, 5, 7…

Para que isso nos ajude de alguma forma, vamos pensar em como representar um número ímpar de forma genérica: Um número par menos uma unidade ou mais uma unidade.

Lembre-se que um número par é sempre um múltiplo de dois.

Bem, a diferença entre as duas representações que acabamos de encontrar é que na primeira nós começamos a sequência dos números ímpares pelo número 1, já na segunda começamos a sequência dos números ímpares pelo número 3. De acordo com nosso problema, vamos utilizar a segunda.

Na expressão {2n+1}, {n} indicaria a posição que determinado número ímpar ocupa na sequência, mas aqui ele a medida (quantidade de triângulos) em cada lado do hexágono. No fundo é quase a mesma coisa. Veja:

1ª moldura: {2 \cdot 1+1=2+1=3}

2ª moldura: {2 \cdot 2+1=4+1=5}

3ª moldura: {2 \cdot 3+1=6+1=7}

E assim por diante!

Ainda falta uma coisinha. Um hexágono possui seis lados, logo, nós precisaremos multiplicar nossa expressão por seis para obter uma lei de formação que descreva a quantidade total de triângulos por moldura.

Para vermos se funciona, basta contar a quantidade de triângulos em cada moldura e depois verificar se a quantidade bate com a obtida na conta.

1ª moldura: {12 \cdot 1+6=12+6=18}

2ª moldura: {12 \cdot 2+6=24+6=30}

3ª moldura: {12 \cdot 3+6=36+6=42}

Viu só? Agora, como queremos saber a quantidade de triângulos na 12ª moldura, basta que façamos {n=12}.

12ª moldura: {12 \cdot 12+6=144+6=150}

Logo a resposta para o nosso problema é que em na 12ª moldura haverá 150 triângulos.

Método 02: Construa uma tabela e busque um padrão.

Talvez você não se lembrasse como representar um número ímpar de forma genérica, ou nem pensasse nos lados das molduras, mas sim na quantia total de triângulos. Nesse caso vamos construir uma tabela e buscar por um padrão (de crescimento, no caso).

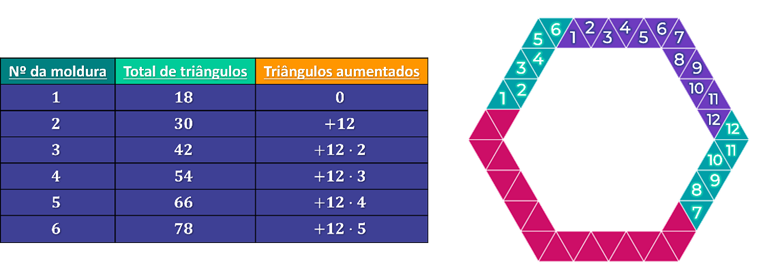
Veja que os aumentos de 12 foram pensados sempre sobre a primeira figura (que já tinha 18 triângulos). Como ilustra o desenho ao lado, foram necessários a primeira moldura mais 12 triângulos para formar a segunda e mais 12 para formar a terceira moldura.

Nisso, podemos focar nossa atenção para esta parte da tabela:

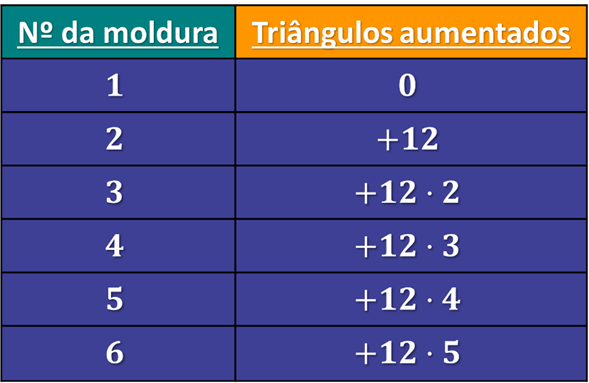
Aqui podemos perceber que a quantidade 12 é acrescentada uma certa quantidade de vezes ao longo da sequência. Essa quantidade é sempre igual ao número da moldura menos uma unidade. Exemplo: 2ª moldura aumenta uma vez a quantia de 12; 3ª moldura aumenta duas vezes a quantia de 12; 4ª moldura aumenta três vezes a quantia de 12 e assim por diante. Dessa forma podemos fazer a seguinte generalização a respeito do quanto é aumentado:

Porém, esse aumento é feito sobre a primeira figura, que já tem 18 triângulos. Dessa forma:

E recaímos sobre a mesma lei de formação do método anterior. Dessa forma, basta que troquemos {n} por 12.

Consegue perceber a questão da variedade que comentei no início da solução? Isto é incrível! Vamos a mais um método!

Método 03: Pense certo com figuras erradas.

O desafio nos propôs pensar a respeito de molduras hexagonais, mas nada nos impediria de investigar esta sequência a respeito das quantidades de figuras por moldura com outras configurações. Observe:

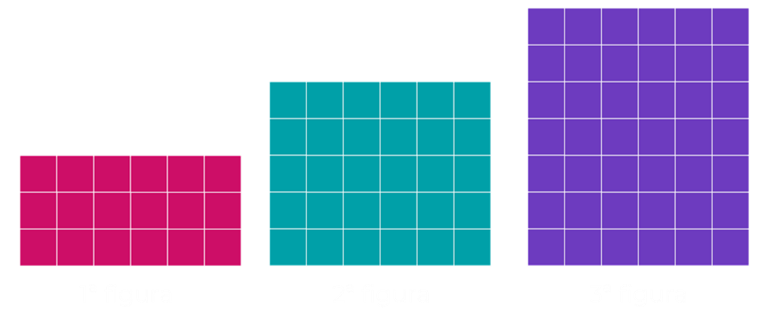
Observe que troquei as figuras por retângulos com a mesma quantidade de figuras.

Um dos benefícios que a configuração retangular nos apresenta é que nós podemos calcular o total de quadradinhos que compõem a figura através do produto das medidas dos lados.

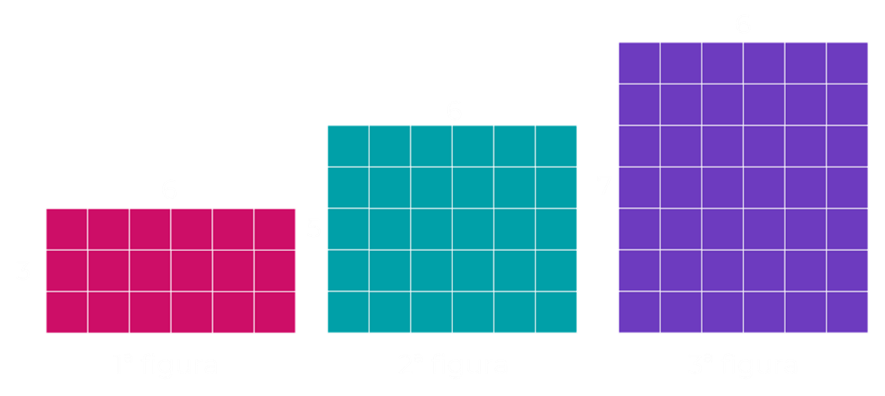
Veja que o número 6 se repete em todas as figuras, então já podemos supor que toda figura será multiplicada por 6. Falta associarmos a cada posição da figura o número da lateral.

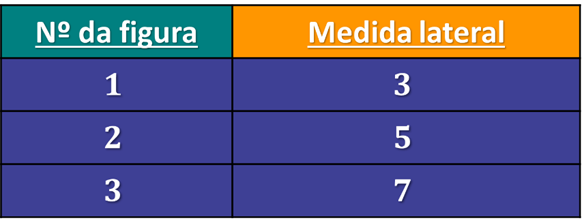
Aqui podemos ver que a sequência dos números ímpares é formada novamente. Nós podemos associar que a cada figura sua lateral será igual seu dobro mais um. Dessa forma:

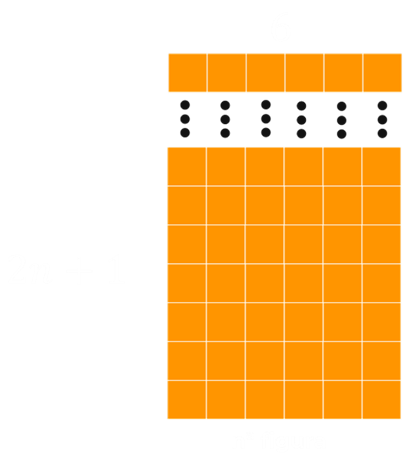
Acima temos uma figura genérica com a nova configuração. O total de quadradinhos será dada pela expressão:

E voltamos a mesma lei de formação vista anteriormente nos outros dois métodos. Por fim:

A 12ª moldura possui 150 triângulos.

Os vários caminhos para resolver um mesmo problema nos permite abrir a mente para conseguir aprender de fato uma nova habilidade!

E você, tinha conseguido resolver este desafio? Como você fez? Espero que tenham gostado das soluções propostas.

Até o próximo artigo. O desafio 12 já está lançado!