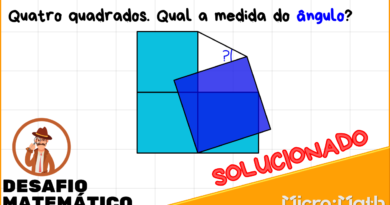
#Desafio 10: Solução

Calcule a área da região pintada considerando a medida do raio igual a 4 cm. Dê a resposta utilizando a constante {\pi}.

Hoje vamos resolver o desafio proposto na semana do dia internacional da matemática.

Ele nos apresentava um problema de áreas muito curioso envolvendo o círculo recortado em algumas partes.

Método: Reconstitua a cena.

A figura original era um círculo laranja antes de sofrer algumas decomposições/ recortes. Este método baseia-se observação e da reconstituição da figura comparando o que ela era inicialmente e como ela ficou agora, ou ainda quais figuras compõem o novo desenho.

Então vamos considerar que uma primeira alteração no círculo original foi esta:

Sendo assim, podemos perceber que do círculo maior foi retirado {\frac{1}{4}} de sua área total, então só utilizaremos {\frac{3}{4}}:

Agora vamos retomar o desenho proposto pelo desafio e replicar as alterações que possuem um formato de semicírculo.

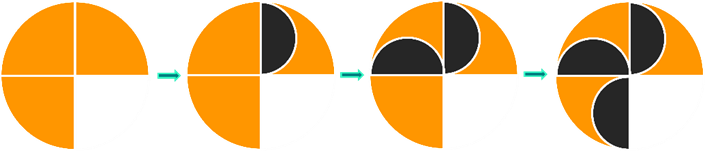
As alterações realizadas correspondem a três semicírculos de diâmetro conhecido. Se prestarmos bastante atenção, o diâmetro dos semicírculos corresponde ao raio do círculo original, ou seja, 4 cm (isso faz com que o raio seja de 2 cm).

Então se juntaremos estes recortes, nós teríamos uma área faltante (que foi recortada) correspondente a um círculo e meio de raio 2 cm.

Como a área do recorte é uma área que foi removida do círculo original, nós só precisamos realizar uma subtração:

Dessa forma conseguimos determinar que a área (laranja) do círculo apresentado pelo desafio após algumas alterações é de {6 \pi \ cm^{2}}

Muito obrigado por terem acompanhado mais este desafio, o próximo já foi lançado.