#Desafio 07: Solução
Cada linha de triângulos aumenta dois triângulos em relação a linha anterior. Qual o número total de triângulos nas vinte primeiras linhas?

Após algum tempo sem postar nenhum conteúdo estamos retomando nossas atividades!
O Desafio 07 apresentava um problema clássico de sequências que envolve números ímpares. Nós temos mais de 10 formas de solucionar este problema, porém aqui neste artigo, irei apresentar somente duas, mas caso você tenha encontrado um outro caminho, por favor, comente logo abaixo do artigo para sabermos como você pensou!
Antes de mostrar um primeiro (possível) método de solução deste problema, vou contar-lhes uma história.
No início do século XIX, pouco após a Revolução Francesa, o mundo conheceu o maior matemático de seu tempo (ou de todos os tempos), o alemão, Carl Friedrich Gauss (1777 – 1855).

Diferentemente de todos os matemáticos franceses que estiveram presentes durante a Revolução Francesa (como Monge, Lagrange, Laplace, Legendre, Carnot e Condorcet) Gauss (como nos referiremos a ele), foi uma criança prodígio.
Seus pais não tinham escolaridade, e por incentivo de sua mãe, Gauss se manteve firme em seus estudos (ainda bem) e no início ele frequentou a escola local, onde o professor era tido como muito exigente. Um dia, para manter a turma ocupada, o professor mandou que os alunos somassem todos os números de um a cem e, após ter encontrado o resultado, era para deixar suas anotações sobre sua mesa, com todo o raciocínio seguido até encontrar tal resultado. Quase que imediatamente Gauss colocou seu caderno sobre a mesa, dizendo, “aí está”; o professor olhou para ele com pouco caso enquanto os outros alunos trabalhavam bastante para obter uma resposta. Quando o professor olhou os resultados de todos, as anotações de Gauss eram as únicas a conter a resposta correta, sem nenhum cálculo. O garoto de 10 anos calculou de cabeça a soma da progressão aritmética {1+2+3+4+...+100}.
No mínimo fantástico, não? Vamos analisar um dos possíveis caminhos que Gauss seguiu para obter a resposta correta. Vamos escrever “todos” os números de um a cem.
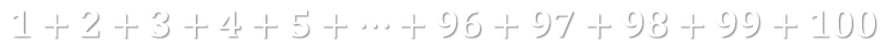
Com isso, vamos calcular algumas somas parciais utilizando como parcelas os extremos desta linha e vamos observar se conseguimos encontrar algum padrão.
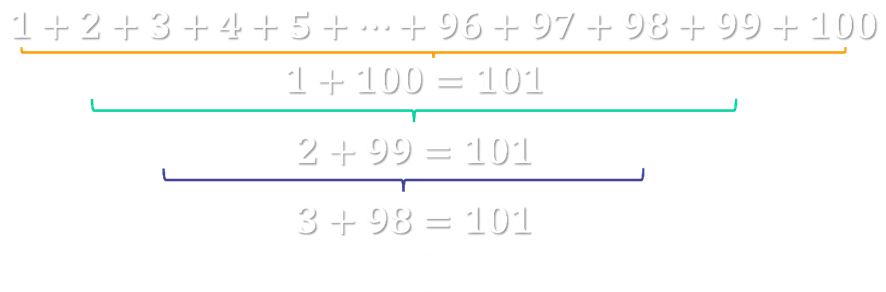
Bem, cada soma que fizemos (e continuarmos fazendo) iremos obter como resultado 101. Ora, agora podemos realizar uma pequena análise da situação:
- São 100 números (um a cem).
- Cada par extremo, quando somados, resultam em 101.
- Temos no total 50 pares
Logo, a soma de um a cem pode ser expressa como:
Com toda certeza o pequeno Gauss foi considerado como prodígio com motivos de sobra.
Tá, mas o que essa história tem a ver com o nosso problema? Bem, sem mais delongas vamos ao primeiro método:
Método 01: “Adição Gaussiana”
O vigésimo número par é 40, logo o vigésimo número ímpar é 39, ou seja, na vigésima linha temos 39 triângulos.
Se considerarmos os vinte primeiros números ímpares sendo 1, 3, 5, 7, …, 39; podemos organizá-los em uma soma:
Somando os números de modo a formar pares com as parcelas extremas da nossa soma, teremos o seguinte padrão:
E assim por diante…
Da mesma forma que analisamos o problema de Gauss, nós agora temos 20 elementos organizados em 10 pares, cuja soma é 40. Logo, a quantidade de triângulos das vinte primeiras linhas é dada por
Método 02: Trabalhando com casos simples
Como já de costume de outros desafios, vamos construir uma tabela para análise de padrões:
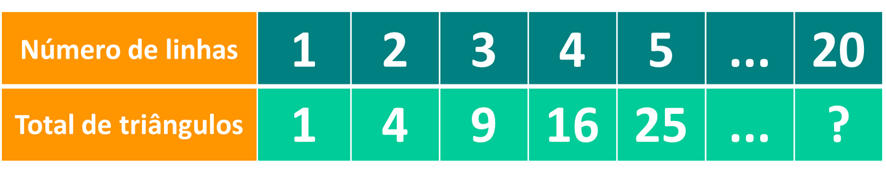
Observe a relação encontrada os números de cada coluna:
E assim por diante…
O total de triângulos até certa linha é igual ao quadrado do número que representa essa determinada linha. Utilizando este padrão, nas primeiras vinte linhas nós teremos um total de {20\cdot20=400} triângulos.
Interessante, não? Se você conseguiu chegar a esse resultado (independente do caminho seguido) deixe me saber como foi.
A respeito do padrão encontrado no Método 02, nós consideramos como verdadeiro pois funcionou para alguns bons casos como vimos na tabela, mas será que ele funciona para uma infinidade de casos? Um artigo novinho em folha está saindo do forno para explicar como podemos provar conjecturas matemáticas e verificar sua veracidade para infinitos casos. Fique de olho!
O Desafio 08 está lançado!



