#Desafio 09: Solução
Uma folha quadrada de papel foi dobrada ao meio para formar um retângulo. O retângulo tem perímetro de 24 cm. Qual a área do quadrado original em cm²?

Hoje vamos resolver o último desafio proposto lá no Instagram. Preparados?
O desafio 09 também nos apresentava uma situação geométrica que envolvia noções de área e perímetro. Para resolução deste exercício fornecerei três modos de raciocinar a respeito.
Método 01: Compare as dimensões do retângulo.
Se relacionarmos as duas figuras envolvidas (quadrado e retângulo), podemos perceber com certa facilidade de que a medida do comprimento do retângulo é a mesma medida do lado do quadrado original e a medida da largura do retângulo é metade da medida do lado do quadrado original.
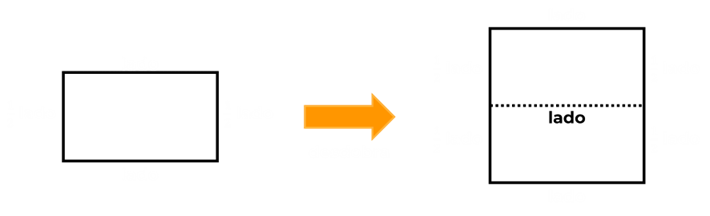
Sabendo que o perímetro do retângulo (informação fornecida) é de 24 cm, podemos relacioná-lo com as medidas do quadrado conforme mostra a ilustração acima.
Logo o perímetro do retângulo é 3 vezes maior do que o lado do quadrado, por isso:
Então a medida de um lado do quadrado é igual a 8 cm, por tanto sua área é calculada por:
Método 02: Trace linhas convenientes.
Vamos dobrar o papel mais uma vez, fazendo com que o retângulo se torne um quadrado novamente. Desdobrando a folha veremos que a folha original se dividiu em quatro quadradinhos congruentes. Chamando de u (unidade) o lado deste quadrado, veremos que o perímetro de um retângulo (unindo dois quadradinhos) é de 6 u, sabendo que seu perímetro é de 24 cm, teremos:
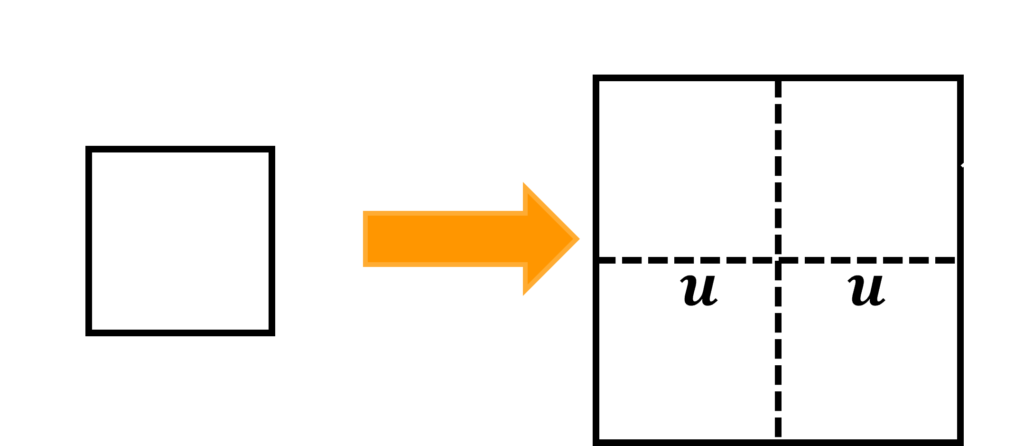
Dessa forma, descobrimos que o lado de um quadradinho é igual a 4 cm, consequentemente a medida do lado do quadrado original é equivalente a medida de dois lados dos quadrados menores, logo, igual a 8 cm. Dessa forma, podemos determinar sua área sendo igual a 64 cm².
Método 03: Use álgebra.
Para evitar o uso de frações, vamos nomear as partes de nosso retângulo (e quadrado) da seguinte forma:

O perímetro de um retângulo é igual a {6\ell} (como na figura), e seu perímetro é de 24 cm. Dessa forma:
Como o comprimento do lado do quadrado é {2\ell}, então {2\ell = 2 \cdot 4 = 8}. Como o lado do quadrado original é de 8 cm, sua área será de 64 cm².



