Por que o parafuso é sextavado?

Olá, de novo. Fico feliz que tenha voltado. Hoje vamos tratar de um ponto muito interessante, que talvez nunca tenha passado pela sua cabeça o motivo, mas que agora deve ter feito você lembrar de todos os lugares em que viu ou usou um parafuso e percebeu que ele possuía um formato hexagonal. Sem mais delongas, vamos começar a nossa discussão matemática sobre esse objeto.

Parafusos são objetos de fixação que são utilizados para a união de peças e suas partes de maneira não permanente, sendo possível também desfazer essa união. Observe o esboço de um parafuso e o nome de suas partes.

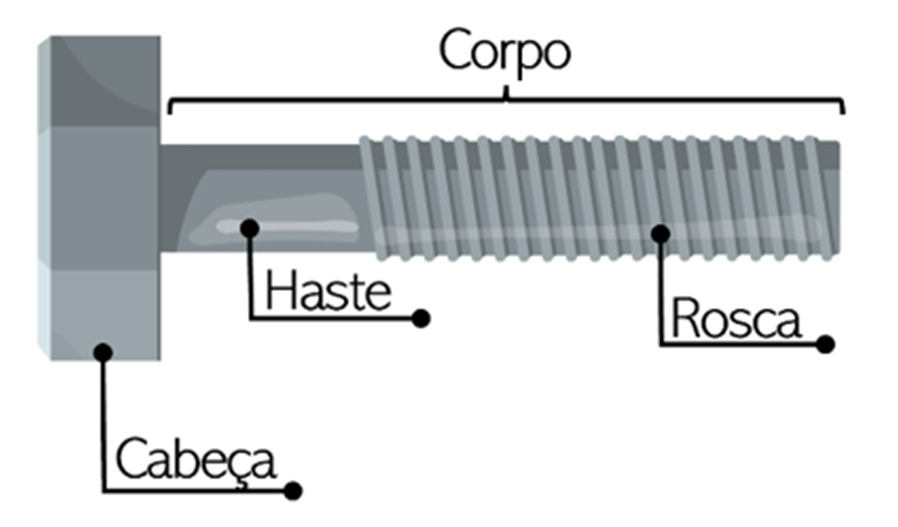
E ainda existem algumas variações quanto ao formato do corpo, pois podem ser cilíndricos ou cônicos, total ou parcialmente roscados e até mesmo parafusos que não possuem cabeça. Como nosso intuito não é trabalhar com os tipos de parafusos, mas sim o motivo do formato da cabeça da maioria dos parafusos serem sextavados, vamos considerar um parafuso com corpo cilíndrico e totalmente roscado.

A cabeça de parafusos comuns (onde se encaixa a chave para apertá-lo ou desapertá-lo) possuem o formato de prismas regulares hexagonais. Mas, por quê? Bom, vamos investigar alguns tipos diferentes de parafuso. Para isto, criei o modelo 3D de cada tipo de parafuso que analisaremos hoje.

Em todos estes tipos de parafuso o polígono presente é sempre regular e é fácil perceber a razão disto. Seria muito inconveniente apertar e desapertar um parafuso cujo formato da cabeça fosse um polígono irregular. A chave precisaria ser especial para aquele tipo de parafuso e ela voltaria a se encaixar nele novamente somente após uma rotação de 360°.

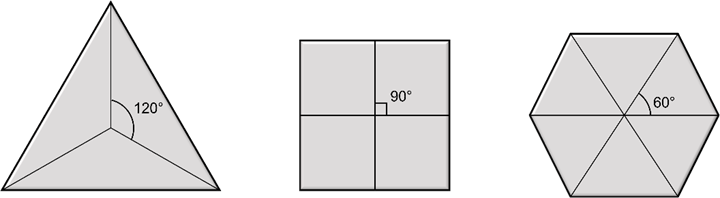
Se o polígono da cabeça do parafuso é um quadrado, após uma rotação de 90°, o parafuso volta à posição inicial, podendo-se encaixar outra vez a chave para um novo giro.

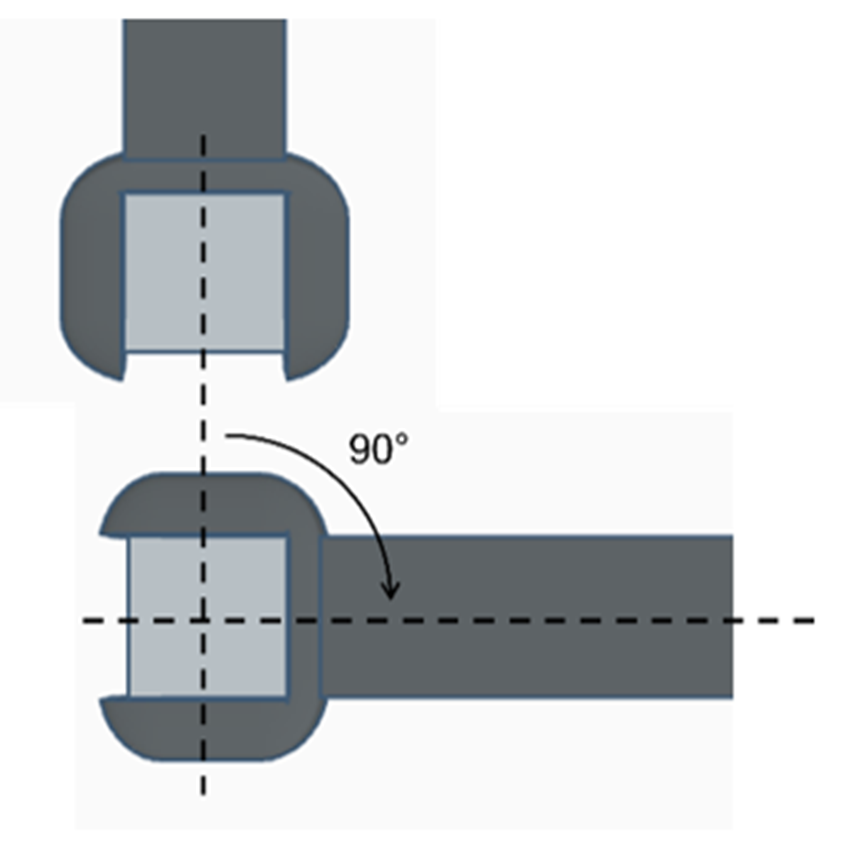
Deste modo com quatro giros de 90° a rosca avança um passo (passo é a distância entre os filetes de rosca presentes no corpo do parafuso).

No caso de um parafuso triangular são necessários três giros de 120° para completar uma volta na rosca (um passo).

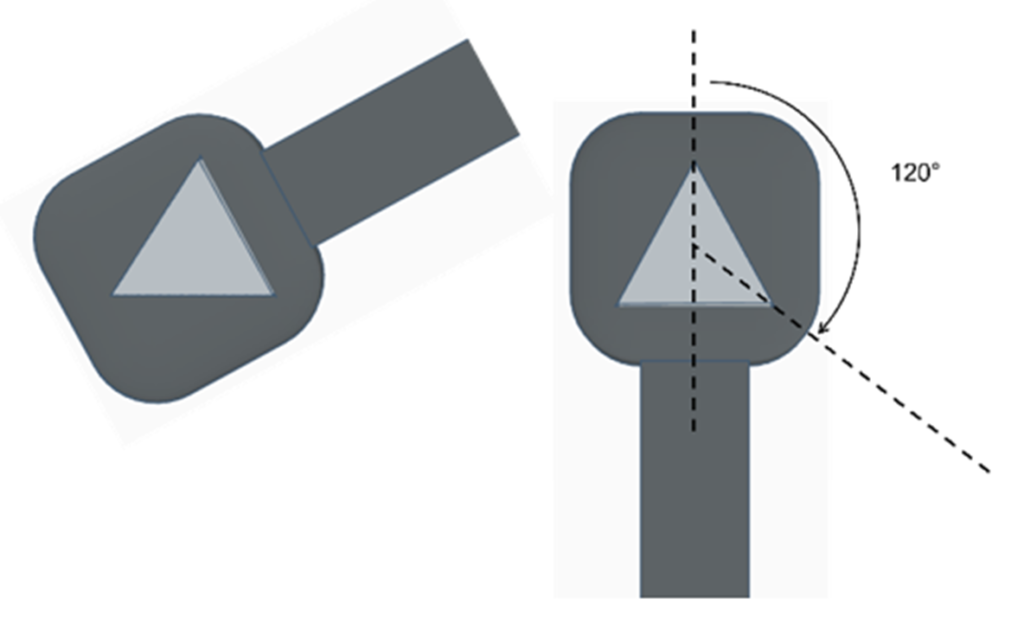
Com o parafuso sextavado completamos um passo da rosca após seis giros de 60° cada um.

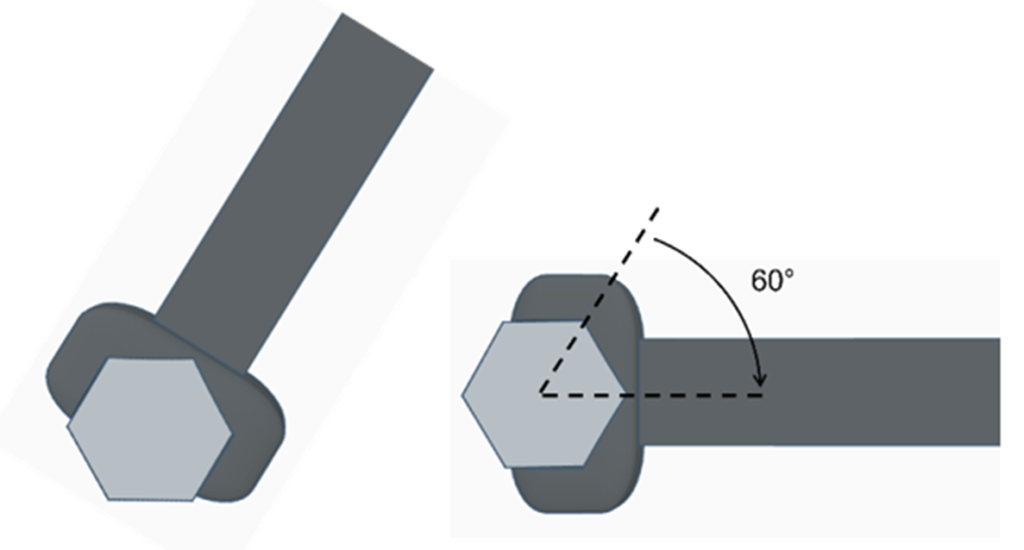
Quando um mecânico ou operário está fazendo algum reparo ou conserto em máquinas, muitas vezes ele tem pouco espaço para trabalhar (em geral em posições desconfortáveis). Por esta razão, dos três parafusos apresentados até agora, o mais cômodo é o hexagonal, pois é o que pode ser apertado (ou desapertado) com giros menores, isto é, com movimentos mais curtos do braço.

Este ângulo que estamos observando ao girar os parafusos é o ângulo central do polígono regular.

A medida do ângulo central do polígono regular de lados é dado pela expressão:

E partindo do pressuposto que quanto menor o ângulo central do polígono regular, menor é o movimento do realizado pelo braço do mecânico, por que não utilizar um polígono com mais lados? Talvez um octógono, por exemplo? Nesse caso o ângulo de giro seria de apenas 45°.

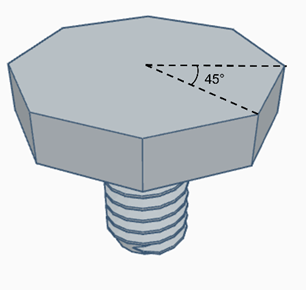
Sem dúvida alguma, sob este aspecto, o octógono é o mais conveniente que o hexágono. Contudo, há outros fatores a serem levados em conta no projeto de um parafuso. O octógono regular está mais próximo do formato de um círculo do que o hexágono regular.

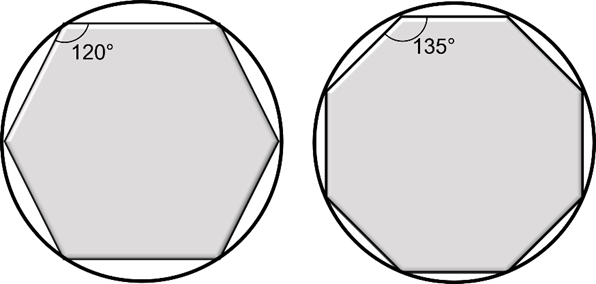
O Ângulo interno do hexágono regular mede 120° e do octógono regular mede 135°. A chave utilizada para apertar ou desapertar um parafuso nunca se ajusta milimétricamente à sua cabeça. Sempre existe uma “folguinha”. Com o decorrer da vida útil do equipamento e das manutenções feitas, a tendência da cabeça do parafuso é sofrer um desgaste e ficar cada vez mais arredondada (dizemos que ela fica espanada). Dessa forma ficaria “impossível” (ou pelo menos, muito difícil) desapertar um parafuso com cabeça octogonal que estivesse espanada. Neste aspecto, o polígono que se sairia melhor seria o triângulo, pois é o polígono que mais se afasta do círculo, tendo o menor ângulo interno medindo 60°.

Perceba que até o momento elencamos duas características para que um parafuso seja funcional: ele precisa se fácil de apertar e desapertar, exigindo menor movimento do braço (ângulo central); a cabeça precisa ter um formato mais distante do círculo quanto for possível (ângulo interno). E até o momento, o hexágono foi o polígono que se saiu melhor nesses dois aspectos.

Mas por que não um parafuso pentagonal? O pentágono regular possui propriedades próximas ao hexágono regular.

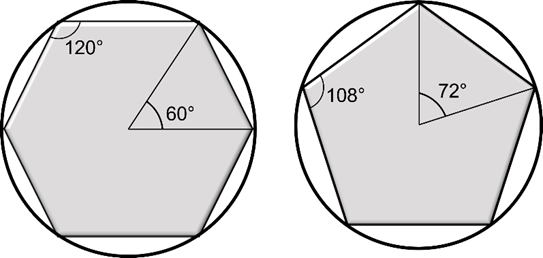
Para compreender por que não existem parafusos pentagonais é preciso considerar um terceiro aspecto. No hexágono regular existem lados opostos paralelos e o mesmo não ocorre no pentágono regular.

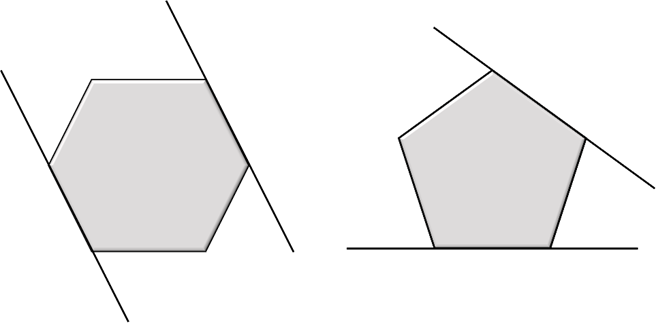
Isto significa que a chave usada para o parafuso hexagonal tem, no encaixe, bordos paralelos, o que facilita o ajuste da chave à cabeça do parafuso.

Para parafusos pentagonais poderíamos ter dois tipos de chaves:

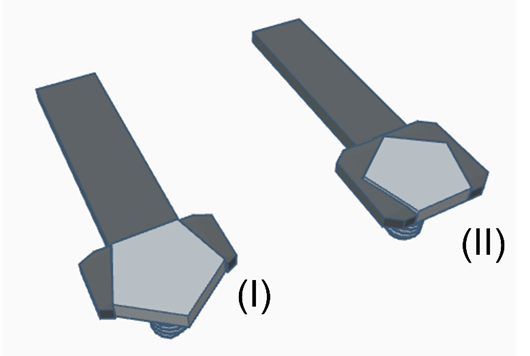
A primeira tem a desvantagem de “escapar” com facilidade e a segunda só se encaixaria na cabeça do parafuso com este movimento:

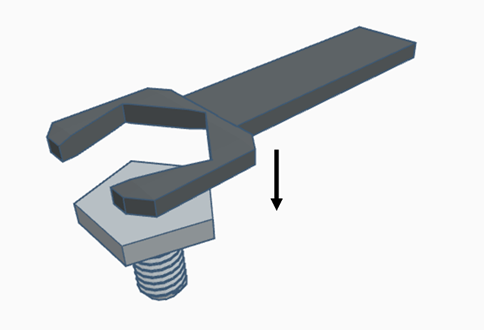
E não com este:

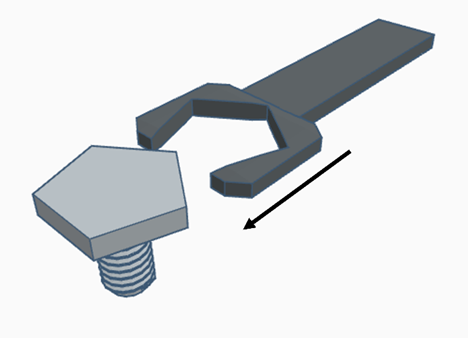
O que acaba sendo incômodo e nada prático para o operário ou mecânico.

Em resumo, no projeto de parafuso com cabeças prismáticas, o polígono regular da base deve ser escolhido levando em conta:

1. Seu ângulo central (giro pequeno);
2. Seu ângulo interno (facilidade de arredondamento dos cantos do prisma);
3. Existência de lados paralelos (encaixe da chave).

Por todos esses critérios apresentados ao longo deste artigo o polígono mais adequado para ser a base do prisma regular (cabeça do parafuso), é o hexágono regular. Muito interessante como toda a geometria que acabamos aprendendo na escola parece tão distante da realidade, mas na verdade ela é usada nas menores coisas e até mesmo em algo tão comum como um parafuso.

Deixo aqui meu agradecimento aos professores Luiz Márcio P. Imenes e José Jakubovic pelo artigo original publicado na 4ª edição da Revista do Professor de Matemática, 1º semestre de 1984, sem eles eu não teria parado para pensar a respeito deste fato tão interessante e devido a maior facilidade dos dias atuais, decidir acrescentar mais imagens e construir modelos tridimensionais dos objetos mencionados para melhor abstração das ideias.

Vejo vocês na próxima, tudo de bom!

REFERÊNCIAS

IMENES, Luiz Márcio P.; JAKUBOVIC, José. Por que o parafuso é sextavado?. Revista do Professor de Matemática. 4. pp. 9 a 11. 1º semestre de 1984.