#DESAFIO 02: Solução
São usados 11 palitos de dente para formar uma fileira com 5 triângulos. Se continuarmos o padrão, qual é o número de triângulos que serão formados se usarmos 89 palitos de dente?

Para este desafio temos várias soluções e irei apresentar duas possibilidades de se pensar sobre este problema.
Método 1: Forme um triângulo por vez.
Os três primeiros palitos de dente formam um triângulo. Depois disso, a cada dois palitos adicionados temos um novo triângulo.
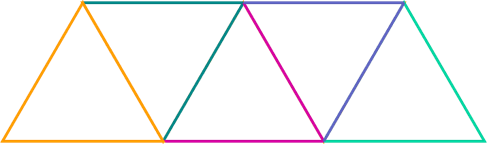
Se pensarmos em utilizar 89 palitos, tiraríamos os três primeiros e ficaríamos com
A cada dois palitos adicionais, um triângulo novo é formado, então
43 pares de palitos são na verdade 43 triângulos formados. Incluindo o primeiro triângulo, nós teríamos um total de 44 triângulos formados utilizando 89 palitos de dente.
Método 2: Construa uma tabela e busque um padrão

Um possível padrão que poderíamos encontrar é que o número de palitos forma a sequência dos números ímpares a partir do 3. E isso nos possibilita de olhar para o padrão apresentado no problema de outra forma.
Como um lado sempre será comum a dois triângulos, podemos separar o desenho de dois em dois palitos e sobrará um palito ao final.
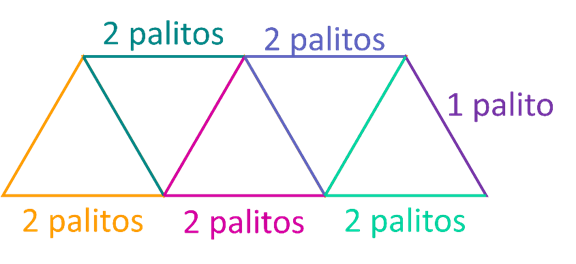
Observe que agora podemos escrever um raciocínio simples com base no desenho acima:
Onde 5 foi o número de triângulos e 11 o número de palitos. O primeiro membro da igualdade acima nos remete a própria representação de um número ímpar genérico. Fazendo algumas alterações na igualdade acima teremos
Onde {t} é o número de triângulos e {p} o número de palitos. Se alterarmos um pouco a expressão
Agora a nossa nova expressão calcula exatamente o número de triângulos montados sabendo-se o número de palitos utilizados.
Ou seja, o número de triângulos possíveis de se montar com 89 palitos de dente é 44.
Percebeu como podemos aplicar diferentes tipos de raciocínios e estratégias para um mesmo problema? Um método me deu um raciocínio mais simples, sem se prender a fórmulas, usando simplesmente um método de contagem mais atento ao padrão proposto. Já o segundo mostrou um método mais analítico do problema, onde eu procurava algo para me basear (padrão) sem exigir muito “esforço”.
Agradeço que esteja acompanhando tudo até aqui!
Fique de olho no #Desafio03!



