A prova dos 9 – Critérios de Divisibilidade
Olá, como vai? Espero que esteja bem. Essa semana iremos tratar de uma curiosidade muito interessante que é como saber se um número é (ou não) divisível por 9. É bem provável que você já tenha ouvido algo do tipo “um número é divisível por 9, quando a soma de seus algarismos for um número múltiplo de 9” ou então “um número é divisível por 9, quando a soma de seus algarismos for 9” e para este último devemos fazer quantas somas forem necessárias até obter um número de um algarismo. E de fato está correto, mas por que este pequeno teorema funciona? É isso que trataremos agora. Vamos pegar os testes demonstrados no post do Instagram:
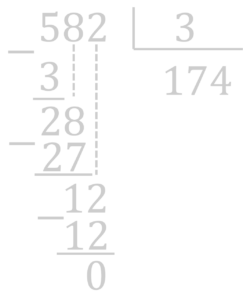
Ao realizarmos este processo, como a primeira soma resultou em um número de dois algarismos, iremos realizar mais uma vez a soma até obter um número de somente um algarismo, buscando que este algarismo seja o 9. No caso, encontramos o número 6, que não é múltiplo de 9. Na verdade, observaremos que 6 é o resto deixado na divisão de 582 por 9.

Podemos realizar o teste com outro número como 1053:
O número obtido foi 9 que, claro, é divisível por 9. Isso significa que o número 1053 é divisível por 9.
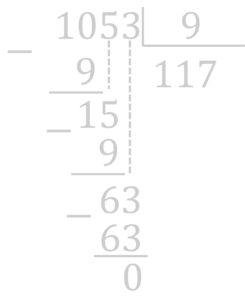
O que está mais do que confirmado, pois a divisão deixa resto zero. Você pode ficar à vontade para testar com quaisquer outros números como, por exemplo 239, 82, 6975 entre outros.
Fazendo uma quantidade qualquer de testes, perceberemos que se a soma resultar em um valor menor do que 9 saberemos que o número original não é divisível por 9 e que esse valor é o resto deixado na divisão deste número por 9. Agora, se a soma resultar exatamente em 9, o número original é divisível por 9, deixando resto zero.
Nós poderemos lançar mão de alguns artifícios algébricos para explicar este comportamento interessantíssimo dos números e demonstrar se esse método realmente funcionará em todos os casos. Então vamos considerar um número qualquer de quatro algarismos {abcd}.
Vamos escrevê-lo na forma polinomial:
Agora vamos alterar, convenientemente, a forma com que o número acima está escrito:
O número 1 foi destacado na escrita acima, para evidenciar o processo realizado. Agora, vamos agrupar os termos da seguinte forma:
A primeira parte da expressão acima nos permite escrevê-la desta forma:
O que evidencia fato desta parte ser um múltiplo de 9.
Vamos analisar a segunda parte da expressão em três etapas. A primeira, em que {a+b+c+d=9}; A segunda, onde {a+b+c+d<9}; E a terceira, quando {a+b+c+d>9}.
1ª etapa: {a+b+c+d=9}
Se a soma dos algarismos for igual a 9, já poderemos considerar que o número original {abcd} é divisível por 9.
2ª etapa: {a+b+c+d<9}
Se a soma dos algarismos for menor do que 9, então ela será equivalente ao resto da divisão do número original por 9, como já vimos no início do artigo.
3ª etapa: {a+b+c+d>9}
Se a soma dos algarismos for maior do que 9, ela assumirá, necessariamente, a forma de um número com duas ordens decimais, isso deve-se ao fato de que {a}, {b}, {c} e {d} assumem, na igualdade acima, a função de algarismos, sendo 9 o maior valor possível para cada variável assumir ({9+9+9+9=36}). Podemos escrever a soma como:
Destaco mais uma vez que cada letra está assumindo um valor posicional. Sendo assim, posso escrever o número {xy} na forma polinomial também.
Vamos alterar, também de forma conveniente, a escrita acima:
Como vimos, {9x} admite 9 como fator, logo ele é divisível por 9. Vamos analisar em algumas etapas os casos para {x+y=9} e {x+y<9}.
1ª etapa: {x+y=9}
Se a soma for 9, então o número original é divisível por 9.
2ª etapa: {x+y<9}
Se a soma for menor do que 9, então ela equivale ao resto da divisão do número original por 9.
O caso {x+y>9} neste momento não nos interessa, pois, a única forma da soma ser maior do que 9 e divisível por 9 é se {x=y=9}.
Se o número original escolhido tiver mais do que 6 algarismos, pode ser que seja necessário realizar mais algumas adições até se obter um número com um único algarismo.
E pronto! Verificamos que sempre que a soma dos algarismos de um número resultar em um múltiplo de 9 (ou a soma da soma resultar no próprio 9) ele será divisível por 9. Nossa, quantos noves…
É claro, no dia a dia você não precisa lembrar desta demonstração ou focar nesses motivos, basta lembrar do pequeno teorema inicial, mas eu acho bem bacana descobrir de onde vem essas coisas bem simples.

Obrigado por acompanhar mais este artigo até aqui.
Até a próxima, e tudo de bom pra você!
REFERÊNCIAS
JOHNSON, Donovan A.; GLENN, William H. Matemática Sem Problemas: Divirta-se com a Matemática. Editora José Olympio, 1972



