O problema da divisão de camelos
Sejam bem-vindos! Hoje é um dia muito especial para a matemática nacional, pois afinal, é o dia Nacional da Matemática! Bom, você deve estar se perguntando: “Se é o dia NACIONAL, o que é que camelo tem a ver com essa história?”. Bem, isso eu te respondo agora!
No dia 06 de maio de 1895 nascia, na cidade de Queluz, Júlio Cesar de Mello e Souza. Ao longo de sua vida se tornou professor, engenheiro e escritor. Lecionou na Escola Normal (escola criada pela corte em 19 de abril de 1879), na Universidade Federal do Rio de Janeiro entre outros lugares. O professor Mello e Souza é responsável por uma série de livros sobre histórias e personagens que contam um pouco da cultura árabe e algumas histórias apresentam a matemática de uma maneira muito interessante e motivadora para quem quer que esteja lendo.

Porém ele fez tudo isso através de um disfarce, publicando seus livros assinando como Malba Tahan, ao invés de seu nome verdadeiro. O professor Mello e Souza desenvolveu tudo perfeitamente para que parecesse que Malba Tahan era um autor de verdade, uma pessoa que tivesse realmente existido. Ele teve a ideia de publicar, em um periódico, contos orientais e educativos de um tal escritor árabe e propôs isso a um diretor deste periódico. Após propor a ideia (ser aceita), os contos começaram a ser publicados na primeira página juntamente com uma pequena biografia de Malba Tahan (ou seu nome completo, Ali Yezzid Izz-edin Ibn-Salin Malba Tahan). Também era divulgado que os contos originais eram traduzidos por um dos colaboradores do jornal, que na verdade era o próprio Mello e Souza escrevendo seus contos através de um pseudônimo, que se sustentou por conta própria e acabou se tornando uma mistificação literária.
Isso é genial, não? O principal personagem do escritor escrevia as “próprias histórias”. É claro que isso foi resultado de muito estudo, por parte do professor Mello e Souza, a respeito dos costumes, cultura, língua e escrita árabe para que, tanto as obras como a biografia de Malba Tahan, fossem convincentes em estilo, linguagem e ambientação.
Caso você se interesse mais pela história deste grandioso autor, basta clicar aqui.
Uma das muitas obras escritas por Malba Tahan, a que mais se destaca, e é nosso objeto de estudo hoje é a intitulada O Homem que Calculava.

Suas outras obras também são muito interessantes, uma boa indicação de leitura. Não estão todas na imagem acima, vale pesquisar sobre as demais. Nelas você encontrará lendas do mundo árabe, histórias de amor, de sabedoria, histórias de monarcas, trabalhadores, príncipes, guerreiros e muitas outras.
Hoje, nós abordaremos uma das clássicas passagens do livro O Homem Que Calculava que é o problema da divisão dos 35 camelos. Esta presente no 3º capítulo (ou 3º ato) do livro. Tomei a liberdade de escrevê-la na integra para que vocês possam ter um gostinho do quão instigante e fabuloso é este livro!

Caso a leitura fique prejudicada pela imagem você pode baixar este capítulo gratuito aqui.
Legal, não? E este é só o primeiro caso que Beremiz Samir resolve ao longo do livro. Mas, isso tudo pode ter te deixado com uma pulguinha atrás da orelha, afinal, como que ele pode feito a divisão de modo que cada um dos irmãos saísse no lucro quanto ao número de camelos e ainda fazer com que sobrassem dois?! É isso que nós investigaremos agora!
Tirando da própria história, os três filhos precisam receber sua herança de acordo com as partes indicadas no testamento de seu pai. Fazendo as contas que os herdeiros fizeram no início da história teríamos que:
Ao mais velho caberia metade da quantidade de camelos, no caso, {17\frac{1}{2}};
Ao do meio caberia um terço da quantidade de camelos, no caso, {11\frac{2}{3}};
Ao mais novo caberia um nono da quantidade de camelos, no caso, {3\frac{8}{9}};
Porém, de acordo com o que foi determinado pelo testador, haveria uma sobra de camelos após a divisão e isso é o que causava desentendimento entre os irmãos:
Se nós somássemos as quantidades cabidas a cada irmão nós encontraríamos um resultado diferente de 35. Veja que a forma como a quantidade de camelos foi dividida entre os filhos gera certo estranhamento, pois ela foi feita utilizando frações, então não nos deixa claro que a divisão dos camelos (nessas proporções) deixa uma sobra e de que essa sobra fosse:
E esta sobra acontece por conta da maneira que foi escolhida para dividir os camelos entre os três herdeiros. Quem se confundiu na divisão (ou esqueceu de avisar que sobrariam camelos sem dono) foi o próprio pai.
O maior problema que este problema apresenta na verdade não é nem a sobra de camelos, mas o uso excessivo de frações. Não que isso seja realmente um problema, mas é muito difícil calcular mentalmente utilizando frações já que não utilizamos frações com frequência em nosso dia a dia. Mas como estamos falando de Beremiz Samir, as coisas mudam um pouco de forma, pois ele é um calculista, ele consegue manipular os números com muita facilidade e precisão. Então antes de seguirmos para o raciocínio desenvolvido por Beremiz, vamos tentar entender essas divisões primeiramente.
Vamos supor que temos uma caixa com 10 bolinhas e queremos entregar metade dessa quantidade para uma criança e um quinto dessa mesma quantidade para outra.
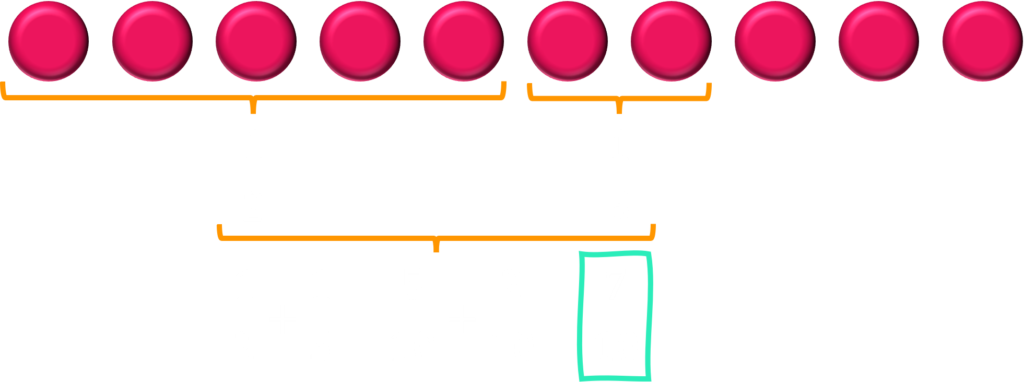
Veja que nesta divisão eu só mencionei quais partes cabiam a cada criança e não especifiquei quantas iriam e muito menos se sobrariam bolinhas, certo? Então de 10 bolinhas, dando metade para uma e um quinto para outra, eu só utilizarei 7 e sobrarão 3. Se fossem 20 bolinhas, sobrariam 6. Consegue perceber a onde quero chegar?
Enfim, retornando ao problema, a sobra que tínhamos era de {1\frac{17}{18}} camelos. Com base nisso, podemos concluir que {\frac{17}{18}=\frac{1}{2}+\frac{1}{3}+\frac{1}{9}} que representam partes do que sobrou e não foram distribuídas aos irmãos. Se nós acrescentássemos essas partes à quantia de cada um dos irmãos, respectivamente, eles passariam a receber um número exato de camelos e ainda sobraria um.
Somando os resultados nós teríamos que {18+12+4=34} e ainda sobraria um já que o total é {35}.
Mas como aumentar essas partes a cada um dos herdeiros sem precisar picotar um camelo?
Graças as habilidades calculistas de Beremiz Samir, ele pôde perceber de antemão que a divisão dos camelos estava numa razão de {\frac{17}{18}}, ou seja, numa situação em que eles tivessem 18 camelos, só seriam utilizados 17, do mesmo jeito que para as bolinhas nós utilizamos somente 7 de um total de 10.
Progredindo nesta proporção teríamos:
Por essa razão, Beremiz emprestou o camelo de Bagdali, para inteirar o denominador da segunda razão acima. Nesta situação em que tivéssemos 36 camelos só seriam utilizados 34, sobrando assim dois camelos: um de bagdali e outro (justificadamente) para Beremiz.
Fantástico como esse problema é abordado com tanta fluidez com a história! Se fosse simplesmente um problema de frações, sem nenhum contexto, talvez fosse muito penoso de resolvê-lo e, com certeza, sem graça nenhuma. Por isso, contar histórias é uma ferramenta tão importante e tão útil para o ensino que o grande professor Mello e Souza já havia percebido isso a quase 80 anos atrás.
O livro conta com muitos outros problemas fascinantes, este é o mais famoso deles. É uma leitura muito gostosa e nada complicada, pois você vai ficar curioso em saber como Beremiz Samir conseguiu resolver aquela situação e como ele pensou e isso só fará você querer ler mais e mais!
Aqui fica registrado minha homenagem a este grande autor e a este dia tão especial para a Matemática. Um grande abraço e até a próxima!



