200%? Como pode passar de 100%?

Talvez essa dúvida já tenha passado pela sua cabeça ou então você já deve ter visto algo como 125%, 200%, 300% nos jornais ou em alguns gráficos, mas o que eles querem dizer? Para isso, convidarei você a embarcar comigo neste artigo onde veremos desde o básico sobre porcentagens até termos condições de respondermos à pergunta inicial. Vamos lá?

Para começo de conversa, uma porcentagem é uma fração de denominador 100. Caso não esteja familiarizado (ou não se lembre) dos termos de uma fração, veja:

Dessa forma, “oito por cento” escreve-se 8% e significa “oito centésimos”, ou seja, {8\%=\frac{8}{100}}. Sempre que se diz “oito por cento” está se pensando em 8% de algum todo-referência pré-determinado.

Em alguns casos, a escrita/ ideia fracionária pode ser simplificada como por exemplo {2\%=\frac{2}{100}=\frac{1}{50}}. Em outros já não, como em {13\%=\frac{13}{100}}.

A ideia de porcentagem é bem antiga, povos de Roma (século I a.C.) já tinham conhecimento deste artifício de cálculo por conta de seu uso no cálculo de impostos.

No final do século XVI, transações comerciais já utilizavam de expressões relacionadas a “por cento” com relação a juros, lucros e prejuízos.

O símbolo para porcentagem como conhecemos hoje (%) é resultado da evolução de uma notação (escrita por extenso e posteriormente escrita na forma de frações) que passou pela mão de diversos matemáticos italianos por volta do Século XVII d.C.

E por conta de o uso de porcentagens estar tão contido na linguagem cotidiana, é muito conveniente termos bem definidos os significados de algumas delas e para isso utilizarei figuras repartidas em 10 partes como um todo-referência para fazer uma correlação mais concreta sobre o caráter representacional da porcentagem.

Outros valores percentuais dão ideias aproximadas sobre a quantidade representada.

Usando as figuras repartidas ficou mais fácil de visualizar a porcentagem como uma representação genérica de partes de um todo que é tomado como referência. Agora, vamos observar o uso das porcentagens no sistema monetário onde nosso todo-referência não é uma imagem, mas sim um valor numérico.

Vamos supor que na venda acima, o pagamento à vista confere 5% de desconto no valor da camiseta, ou seja, será abatido no preço de R$ 69,90 uma quantia equivalente a um vigésimo (5%) deste valor.

Observe que neste caso, por conta de o contexto tratar do sistema monetário, não faz sentido considerar três ordens decimais, por isso apliquei uma regra para arredondamento no valor correspondente a 5% que é a seguinte:

Verifica-se quantas ordens decimais se deseja manter no número. Se o último algarismo for 0, 1, 2, 3 ou 4 nós iremos substituí-lo pelo zero. Se o último algarismo for 5, 6, 7, 8 ou 9 nós arredondamos a ordem seguinte para o próximo numeral assim como fiz no exemplo acima.

Contudo, sempre que possível utilize a maior quantidade de ordens decimais (dependendo do seu contexto) pois excessivas aproximações podem causar variações nos resultados intermediários e influir consideravelmente no valor final. Aqui realizei o arredondamento por uma facilidade de cálculos e fluidez na leitura do artigo.

Retomando o assunto central, veja que não precisamos utilizar de artifícios algébricos ou macetes para determinar o valor correspondente aos 5%, simplesmente compreendemos seu significado.

Agora que temos um melhor entendimento sobre as porcentagens, percebemos que nem sempre fará sentido falar em porcentagens superiores a 100%, pois por exemplo, 120% é o total de referência mais 20% deste total. Um desconto de 120% na mesma camiseta faria com que seu preço ficasse abaixo de zero:

20% de R$ 69,90 (a quinta parte de R$ 69,90):

100% de 69,90 (total) mais os 20% calculado anteriormente teremos 120% de R$ 69,90:

Aplicando o desconto de 120%:

O que é isso?! Eu ganho a camiseta e ainda recebo R$ 13,98 da loja?! (contém ironia).

Contudo, o preço da gasolina é um bom exemplo a se levar em conta devido seus consideráveis aumentos. Este pode sofrer um aumento de 120% e não parecerá um absurdo (mesmo sendo). Por exemplo, o preço de um litro de gasolina é R$ 3,93 e este sofre o aumento de 120%.

20 % de R$ 3,93:

100% de R$ 3,93 mais 20% que é (aproximadamente) R$ 0,80:

Aplicando o aumento de 120% teremos:

Lastimável, mas isso pode ocorrer (como já ocorreu outras vezes…).

Enfim, percebeu como porcentagens maiores do que 100% apresentam o total e mais uma parte deste total?

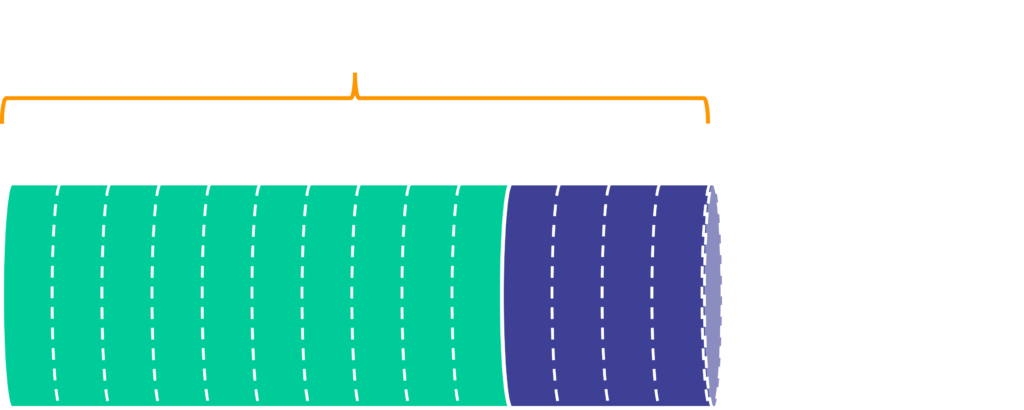
Antes do próximo questionamento, observe a confusão que alguns números como estes podem causar.

Algo custava em torno de R$ 195,00 há alguns anos, mas hoje custa R$ 585,00. Logo, podemos pensar que como {585={3}\times{195}}, o aumento foi de 300%, mas não! O aumento real foi de {585-195=390}, ou seja, {{2}\times{195}}, no caso 200%. Veja que 595 é 300% de 195, mas o aumento foi de 390 somente, logo 200% de aumento.

Ótimo. Agora ficou mais claro como pode-se interpretar porcentagens maiores do que 100? Espero que sim. Mas, ao longo do artigo citei rapidamente sobre a soma de porcentagens. E aí, podemos somar porcentagens de qualquer forma?

Se depender do raciocínio que utilizamos para chegar ao 120% tudo bem, pois tanto 100% como 20% tinham como referência o mesmo valor. Agora observe a situação abaixo:

Observe que os aumentos não ocorrem sobre o mesmo valor. O segundo aumento é feito sobre o novo valor da parcela, ou seja, no terceiro ano de pagamento o valor da parcela não terá aumentado 15%. Vamos observar a situação mais de perto.

Valor de cada parcela:

Valor de cada parcela após um ano:

O valor das parcelas no terceiro ano de pagamento terão um aumento de 8% em cima do último valor calculado.

Esta é a forma correta de se trabalhar com as porcentagens sucessivas. Veja que se eu calculasse um aumento de 15% sobre o valor inicial nós teríamos:

Veja que uma pequena diferença foi gerada. Vamos calcular o quanto foi o aumento percentual real relativo ao primeiro valor da parcela:

Essa última parte da soma se faz necessária, já que o aumento de 8% é feito após o aumento de 7%. Para facilitar nossos cálculos, vamos operar com frações:

Igualando denominadores teremos:

Simplificando a fração por 100 teremos:

Se quiséssemos calcular o valor da parcela do terceiro ano em diante a partir do primeiro valor, deveríamos utilizar 15,56%:

Os dez centavos apareceram neste caso por conta das nossas aproximações.

Espero que tenham compreendido como trabalhamos no caso de aumentos (ou descontos) de porcentagens aplicadas sucessivamente.

Viu só? Por isso é muito importante estarmos atentos ao uso de porcentagens em nosso dia-a-dia, pois se não soubermos o que elas estão representando, qual seu significado (contexto), elas podem nos enganar facilmente. Dizer 25% não traz informação alguma, eu posso estar falando de 25% de 1200 pessoas ou então 25% de 1 200 000 de pessoas e aí a coisa muda totalmente de figura, por isso fica o alerta para o uso e leitura de porcentagens.

Espero que tenha sido instigante e divertido a sua leitura assim como o foi para mim escrever. Qualquer coisa é só deixar um comentário abaixo. Obrigado!